Simulation of Magnetization of Permanent Magnetic Objects in a Customized Fashion -

In this application note, Dr. K.M. Prasad, Senior R & D Engineer with Integrated Engineering Software discusses magnetization of a virgin magnetic material into a permanent magnet in the magnetic solver, AMPERES. In previous versions, only the orientation of different parts of the permanent magnet was customized. Now, in the upcoming version, both orientation and strength of the different parts of the permanent magnet have been customized.

In the model, a piece of a virgin magnetic material in the desired shape was exposed to highly impressed magnetic fields produced by magnetic chargers. Different regions were exposed to different impressed magnetic fields simultaneously so as to obtain a customized pattern of magnetic orientation.

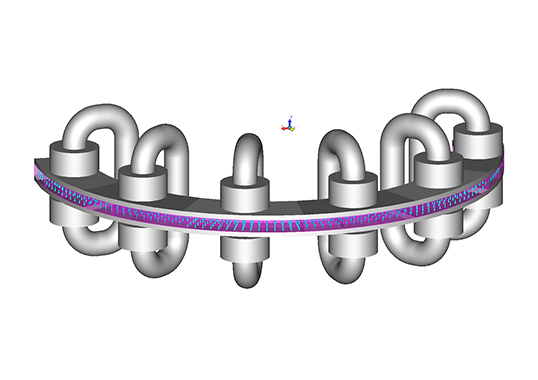
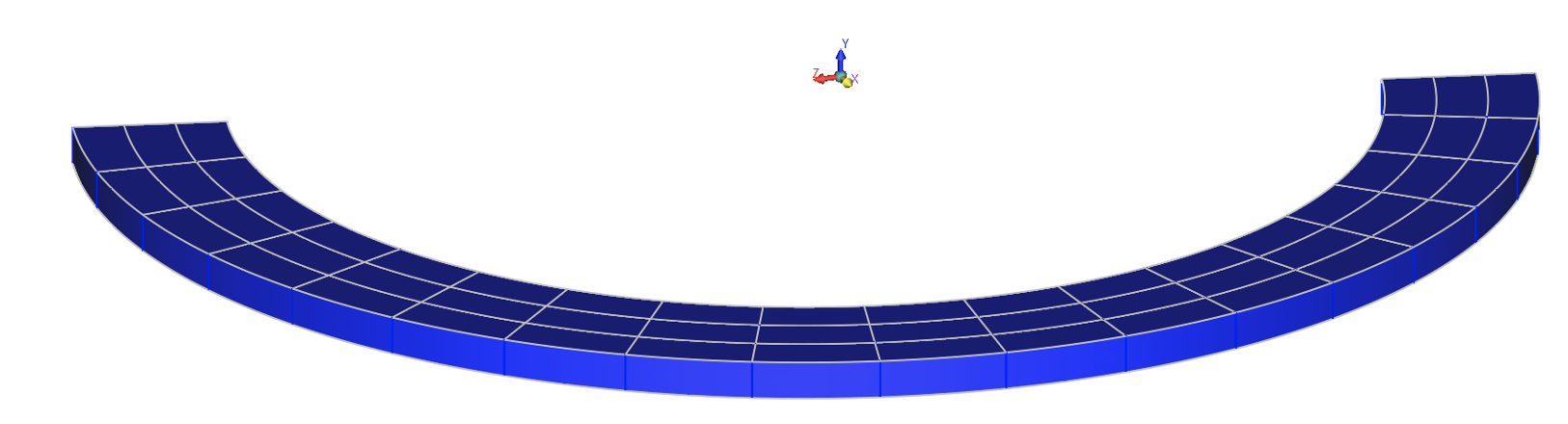
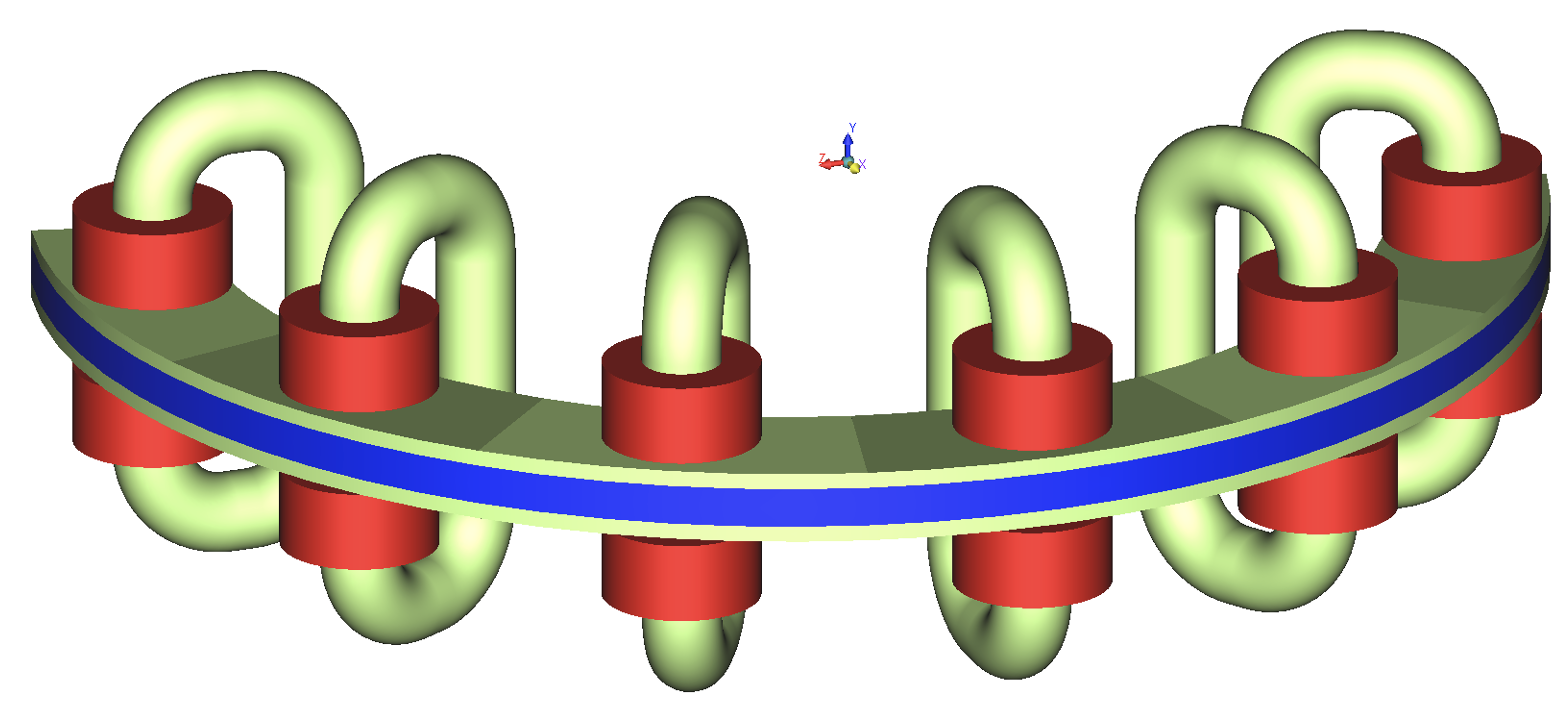
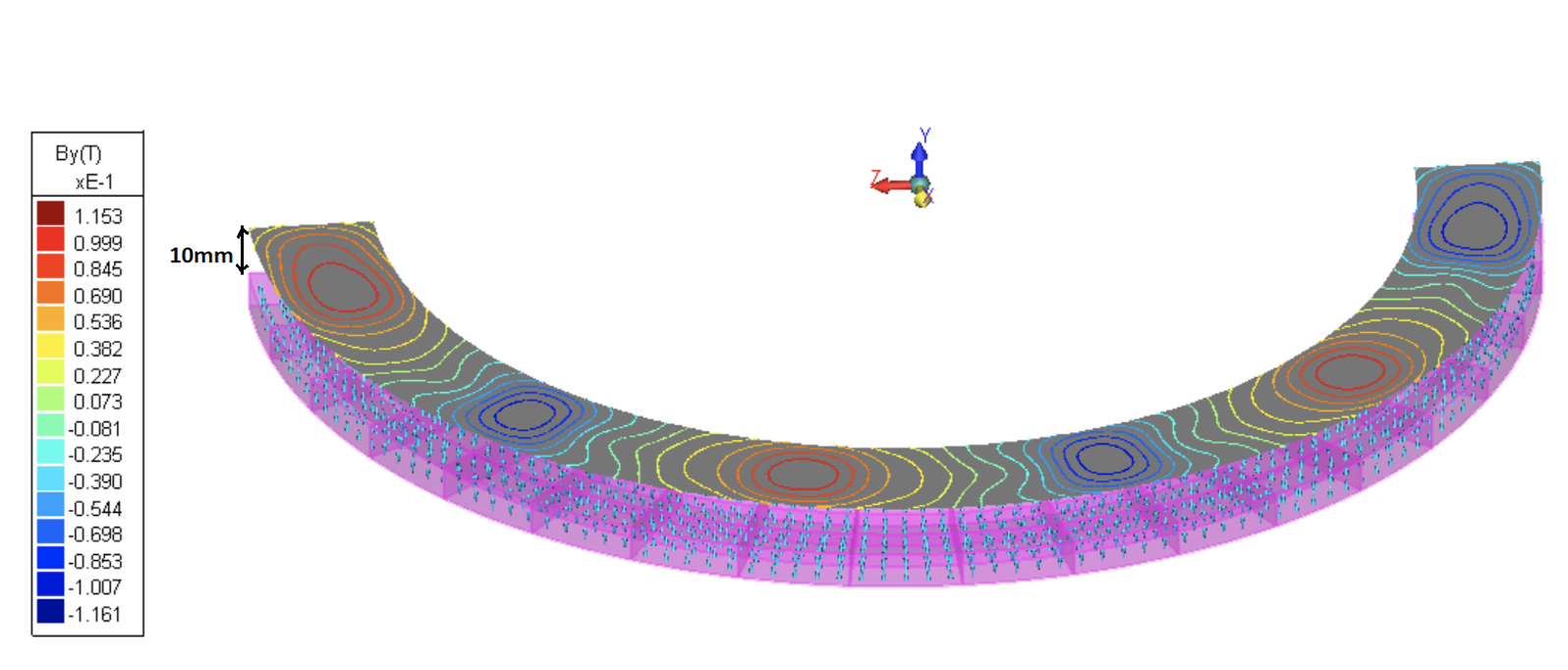
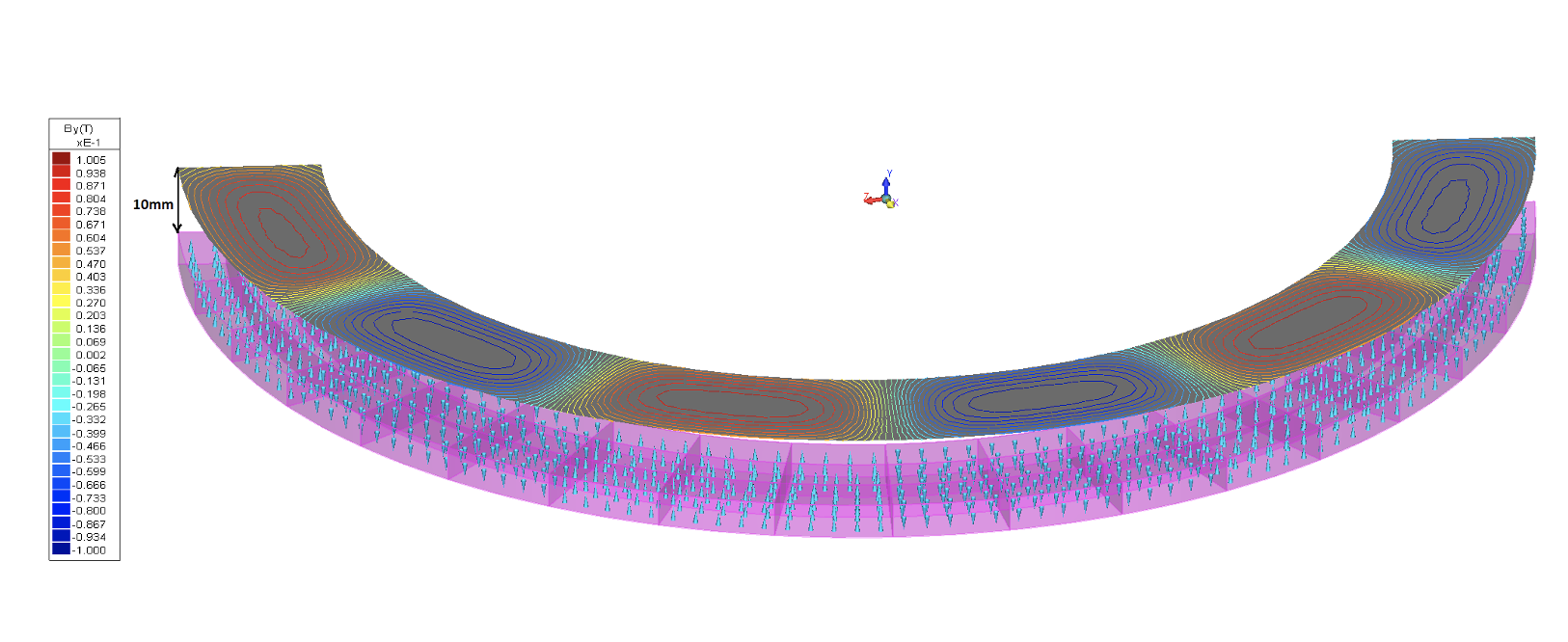
Images show a semi-circular ring magnetized in 6 alternatively reversing magnetization directions oriented along its axis. The angular stretch of each magnetization portion is 30^°. Accordingly, a magnetic charger having 6 sets of coils with alternatingly changing senses of current flow is modeled.

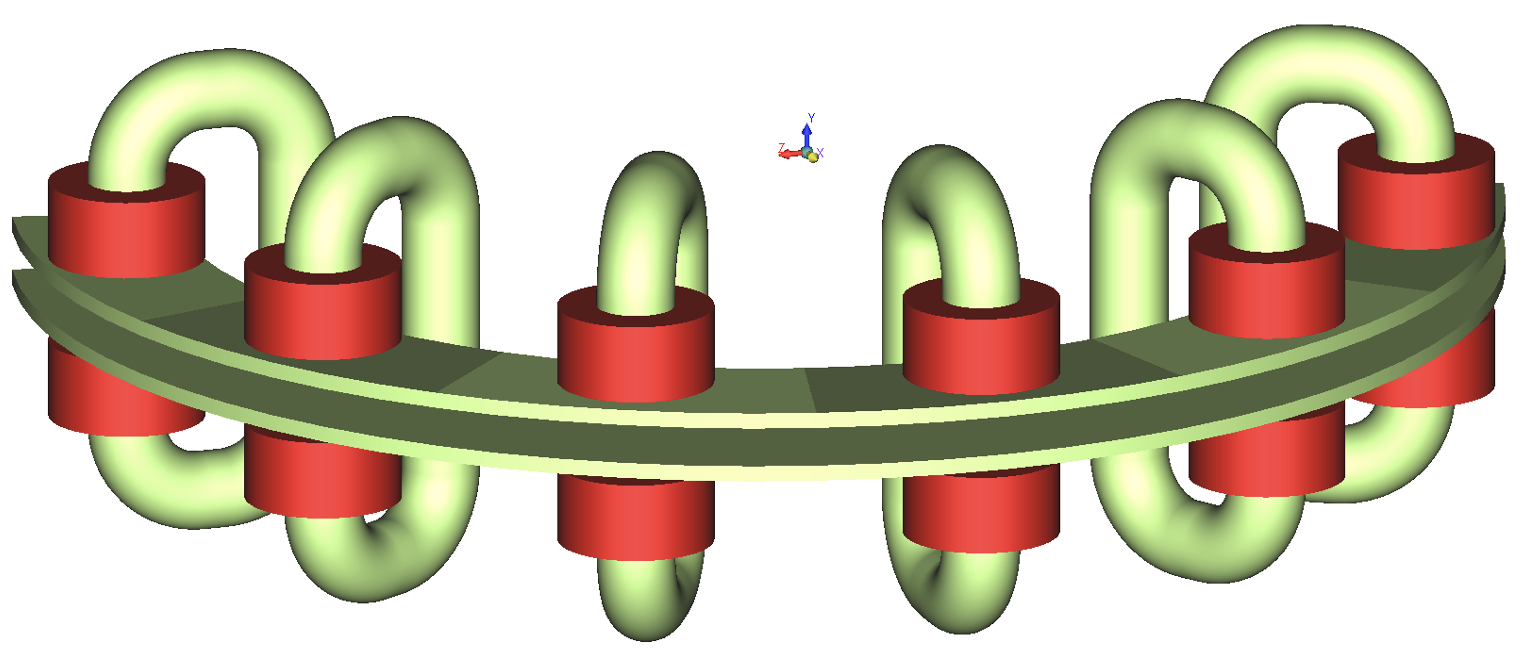
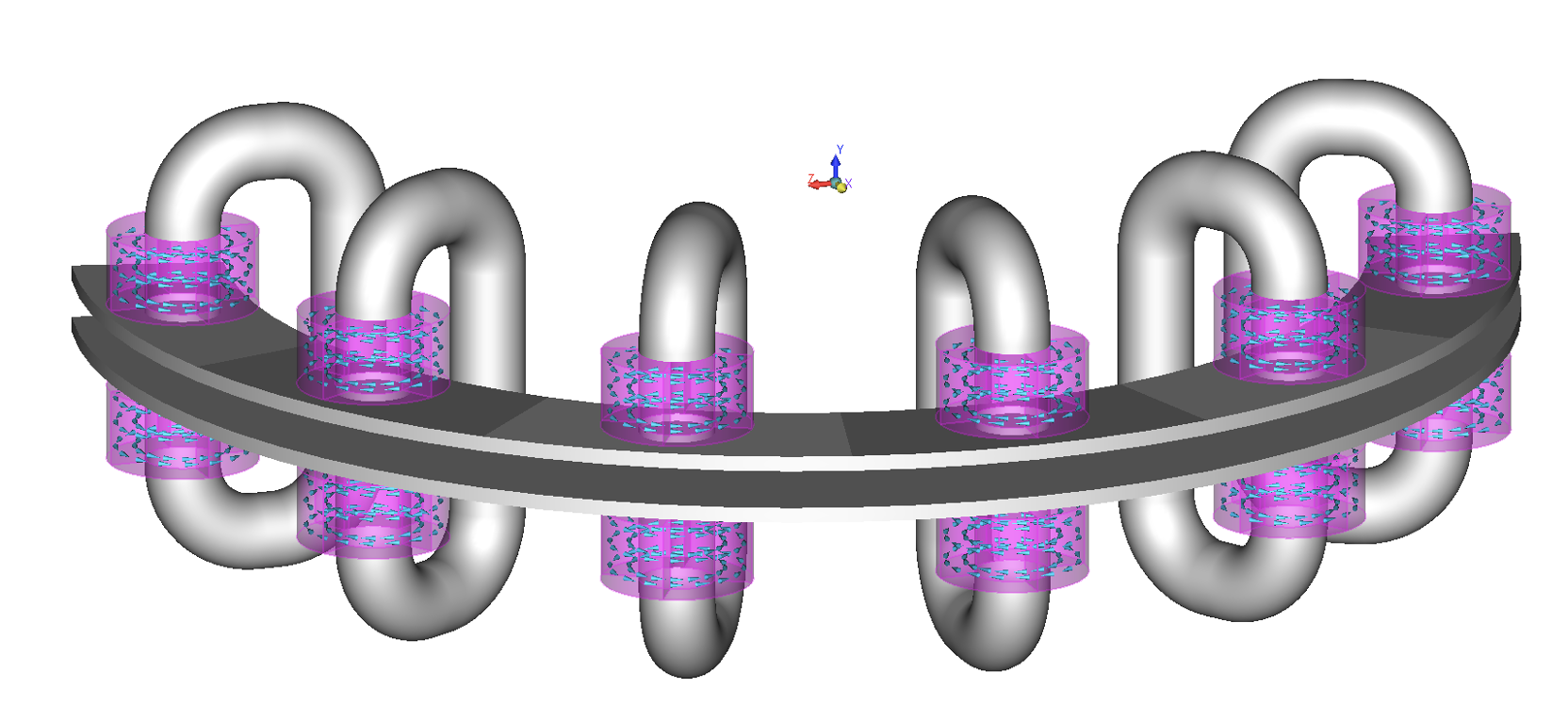
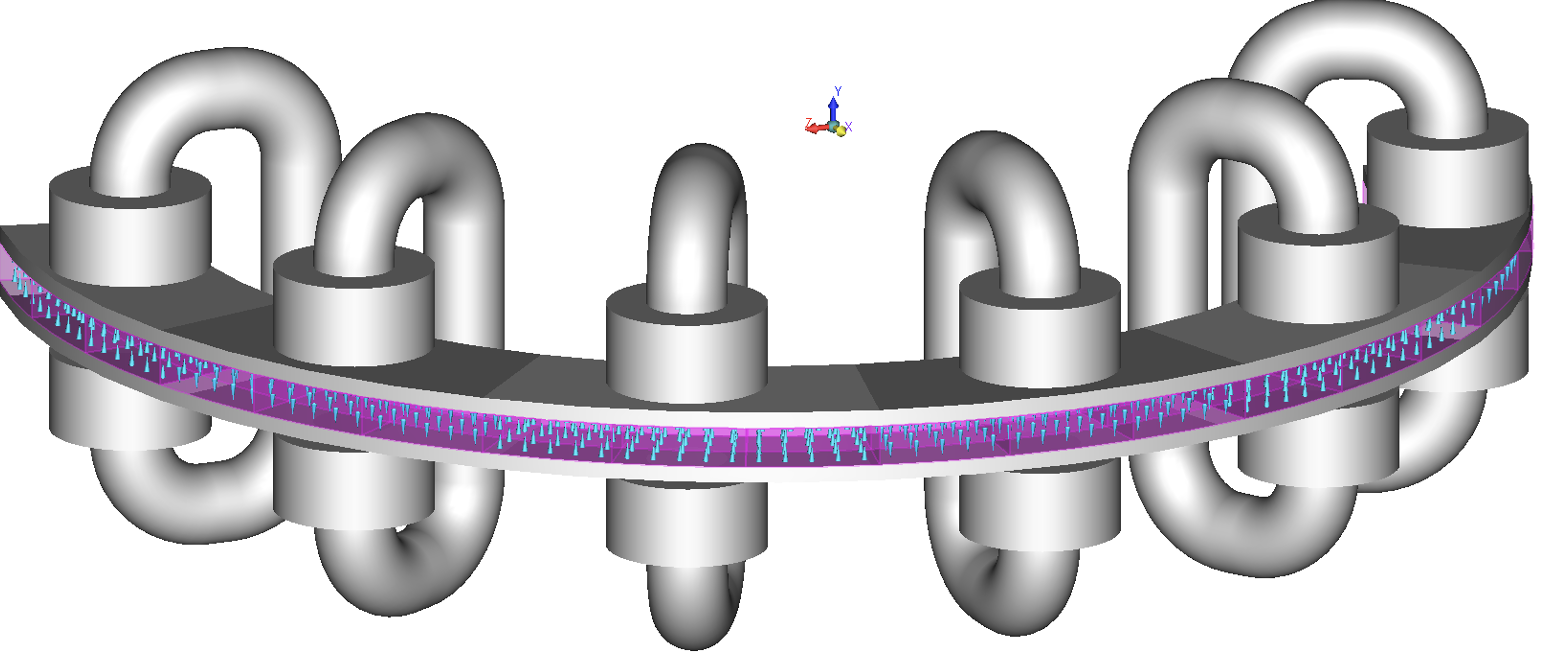
Fig. 3: Semi-circular ring to be magnetized.

The virgin piece of the semi-circular magnetic ring was sandwiched between the charger plates, and appropriate material was assigned to the model. This model was discretized and solved in AMPERES by selecting the command “Magnetize”. Once magnetization has been done, the geometry related to the magnetic charger was deleted and the appropriate permanent magnetic material property was assigned to the semi-circular disk. This model was solved by hitting “Run Solver” to determine the magnetic fields produced by the magnetized ring.

This simulation involved two important actions: first, the material to be magnetized was divided into many smaller volumes since the higher the number of divisions, the greater the accuracy. This, however, should not be more than some required number. In this example, the semicircular ring was divided into 6 equal angular portions and each angular portion was subdivided into 9 smaller volumes, i.e. in total, the semi-circular ring was divided into 54 (=6X9) smaller volumes. The reason for dividing the magnetizing piece into smaller volumes is that AMPERES calculates the magnetic flux density vector (B) at the geometric center of each smaller volume and magnetizes it in the direction of B vector. The program will also assign an appropriate new permanent magnetic material to each smaller volume.

Fig. 4: Semi-circular ring sandwiched between plates of magnetizing charger.

Fig. 5: Permanent magnet directions of discretized volumes of semi-circular ring after magnetized.

The de-magnetization curve of this new material that would be a scaled-down version of the de-magnetization curve of the permanent magnetic material that was assigned to the virgin material. The scaling factor is the ratio of the B field value at the geometric center of the smaller volume to the user-specified minimum B field required to magnetize the virgin material to fullest strength, meaning the permanent magnet will have the vendor specified de-magnetization curve after magnetization.

It is important to note that the magnetic material property of the virgin piece is the same as that of the permanently magnetized piece. For the virgin piece, the magnetic material can be a linear material with a constant relative permeability or a non-linear material specified by a non-linear B-H curve confined to the second quadrant only.

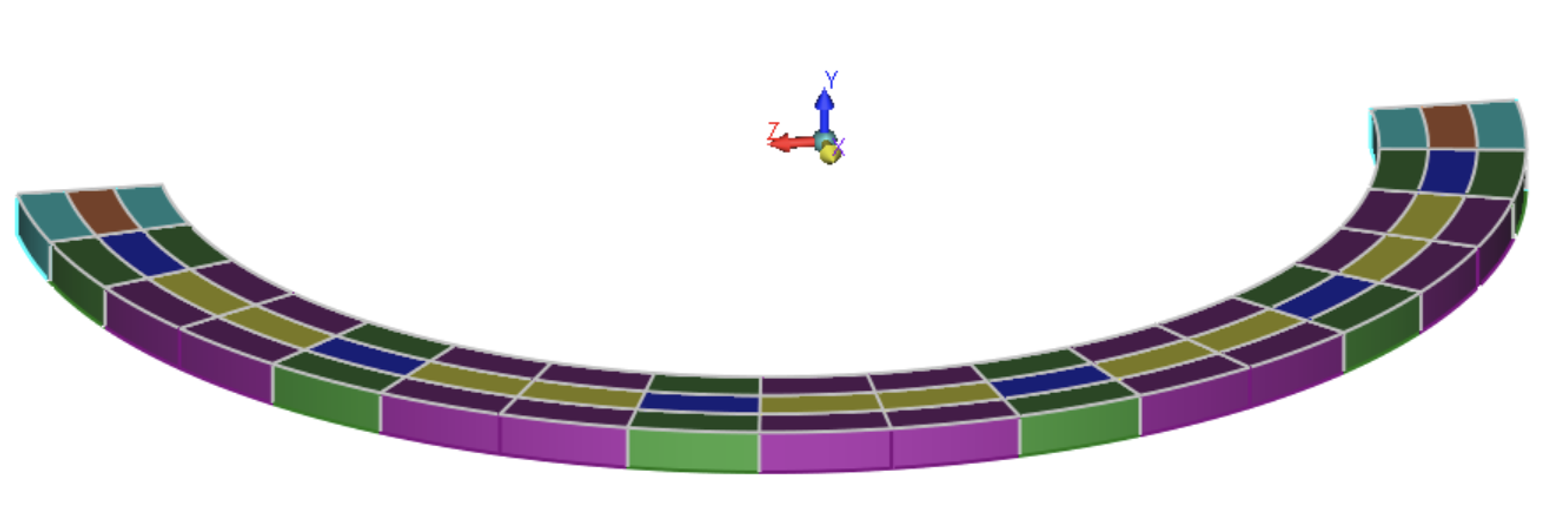
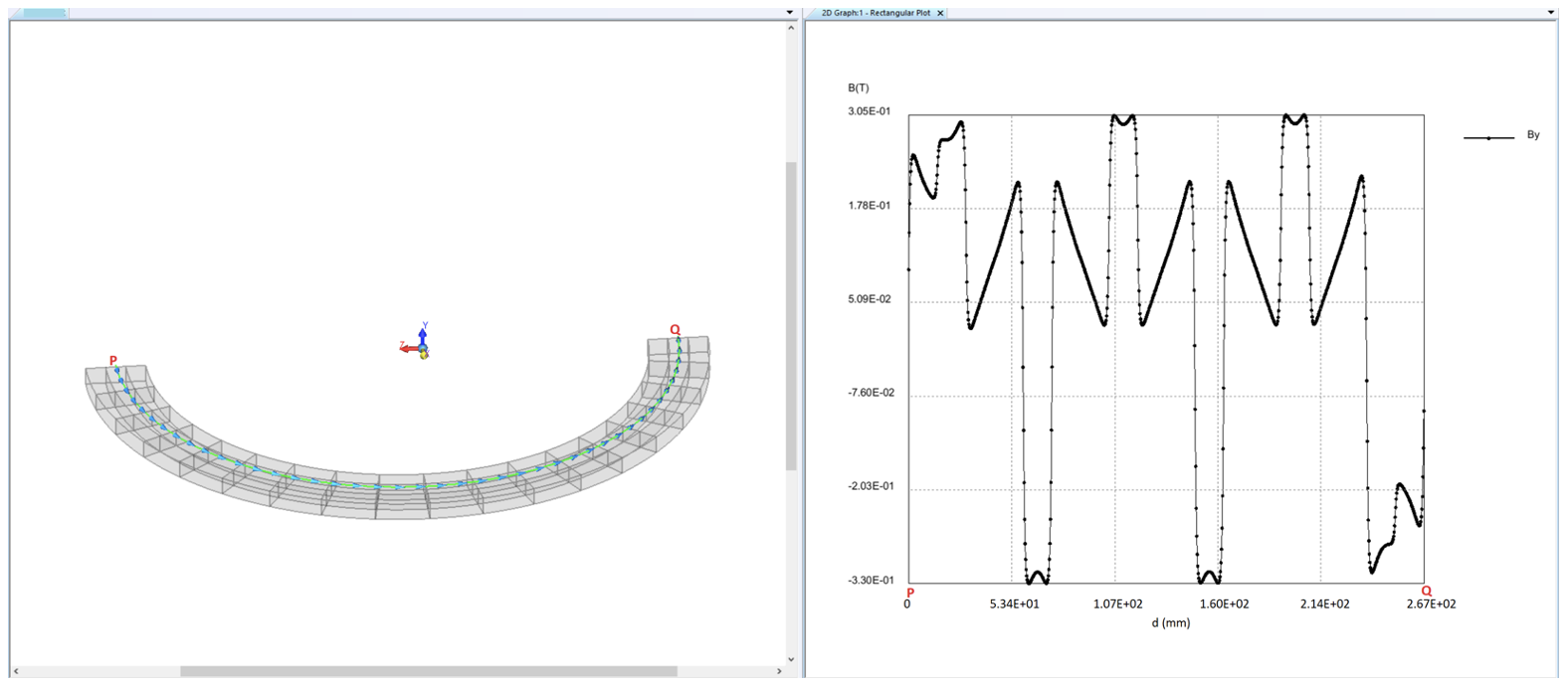
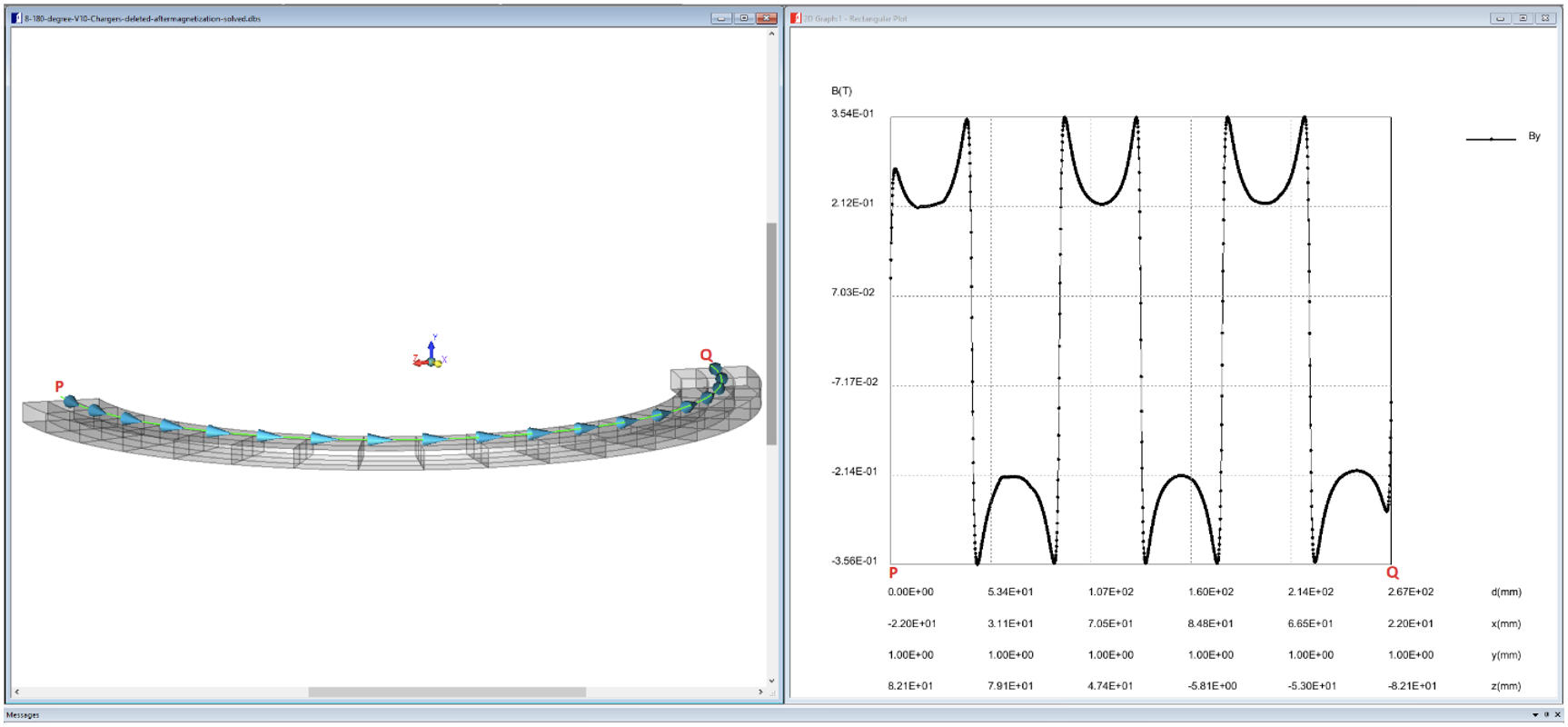
Fig. 6: Minor permanent magnetic materials assigned to discretized volumes after magnetization.

After magnetization is done in AMPERES, the program assigns different minor permanent magnetic materials, which are the scaled-down versions of the permanent magnetic material initially assigned. The B-field results shown in Figs. 7 and 8 are with the minor permanent magnet materials whereas those shown in Figs. 9 and 10 are with the permanent magnet material initially assigned. These results demonstrate the effect of using minor magnetic materials calculated by AMPERES.