Read This Article in English

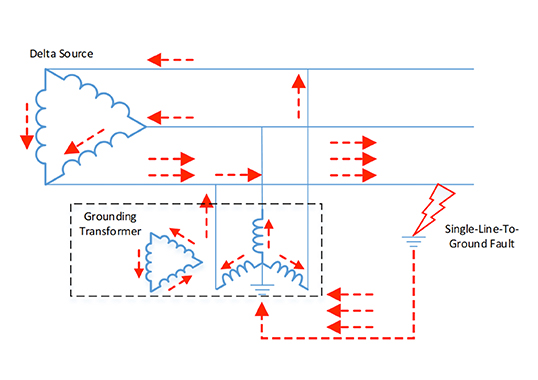
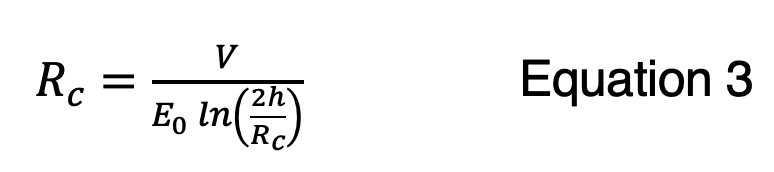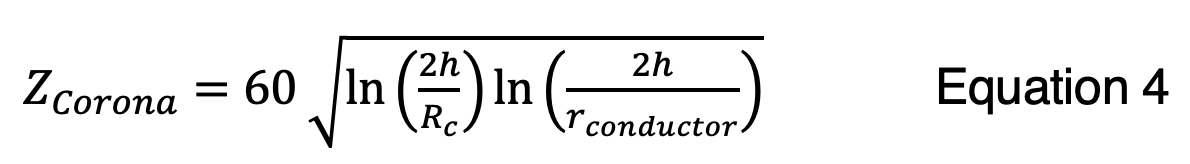A veces, los ingenieros de sistemas de distribución usan el derecho de paso de transmisión existente para trazar los circuitos de voltaje medio (VM) en los casos donde las normas muestran que existe el espacio libre vertical adecuado para los circuitos de transmisión de voltaje alto (VA) de más arriba. A menudo, el desempeño de los circuitos de VA en condiciones de rayos mejora, mientras que la tasa de disparos de los circuitos de VM es decepcionante.

En este artículo del 2019, editado para INMR, el Dr. William Chisholm explica que los pararrayos de línea contra sobrevoltajes ofrecen la posibilidad de mantener los beneficios de un mejor acoplamiento electromagnético de rayo en el circuito de AV de más arriba, mientras se mitigan los sobrevoltajes inducidos y por arco inverso en el circuito de VM de más abajo. Si se realiza la selección apropiada, los pararrayos en el circuito más bajo también pueden mitigar las fallas de contacto de sistemas cruzados.

---

En la Figura n.° 1 se muestra una disposición visualmente atractiva de unos circuitos de transmisión “delta” y circuitos de distribución “horizontales” con 1, 2 y 3 conductores balanceados en cada lado.

Esta línea se protege contra rayos mediante una línea de tierra aérea (OHGW) única montada en la parte superior del poste. Cada poste de acero está conectado a tierra, pero la resistividad del suelo varía considerablemente de torre a torre, por lo que cada poste va a tener un valor diferente de resistencia a pie de torre. Se considerará el desempeño de una estructura con cuatro circuitos en condiciones de rayos, como se indica en la Figura n.° 1. Asuma que los circuitos de transmisión de 115 kV tienen aisladores de 1,0 m y los circuitos de distribución de 50 kV tienen la distancia de arco en seco mínima recomendada de 0,5 m. Esta configuración de la línea se puede utilizar para visualizar el concepto de acoplamiento electromagnético por impedancia de sobrevoltaje. Dependiendo de la distancia de la OHGW única, cada fase tomará una onda de voltaje que sea confiable, pero que es una copia de amplitud reducida de lo que aparece en la parte superior de la torre. La tensión por voltaje de cada aislador es la diferencia entre el aumento local de voltaje de la torre y este voltaje “acoplado”.

La resistencia de aislación de los circuitos de distribución es tan baja que, para la mayor parte de los sobrevoltajes por rayo, algunas de las seis fases o todas generarán un arco eléctrico a tierra. Cada arco eléctrico introducirá un paso nuevo para un rayo, lo que cambiará el acoplamiento. La resistencia del acoplamiento se expresa como un conjunto de “factores de acoplamiento”, C_n, con valores individuales para cada uno de los conductores. En la Figura n.° 1 se muestran doce.

Se realizará una serie de cálculos para establecer un parámetro importante en la “tasa de arco inverso” que establece la tasa de apagones por rayos de la mayor parte de las líneas. Esta es la “corriente crítica” I_crit que hace que el voltaje en uno de los aisladores de línea exceda levemente la resistencia al impulso por rayo, lo que provoca una falla de línea a tierra que sigue al arco eléctrico y lo mantiene.

Se puede obtener un valor estimado de la I_crit al dividir el arco eléctrico crítico del aislador por la impedancia a pie de torre, medida en la base de la torre golpeada por el rayo. En las normas se describen un número de ajustes que son:
• La curva de voltio-tiempo para el arco eléctrico por impulso: por lo general, se hace un cálculo para el tiempo del arco eléctrico en el rango de 1 a 3 microsegundos y el tiempo de evaluación depende de la longitud de las retenidas aéreas.

• El acoplamiento por impedancia de sobrevoltaje de aquellas OHGW con falla y los conductores protegidos con pararrayos que alejan una fracción de la corriente del sobrevoltaje por rayo en cada dirección desde la parte superior de la torre.

• El aumento de voltaje adicional relacionado con el flujo de corriente de aumento rápido en la inductancia de la estructura delgada de un poste.

• La variabilidad de la resistividad del suelo y la impedancia de pie a tierra de estructura a estructura.

• Los efectos de corona, que absorben la energía de los rayos y reducen la tensión en los aisladores.

• Los efectos del voltaje de línea, ya que una fase siempre tendrá un voltaje instantáneo que se agrega a la tensión.

• Los efectos de los pararrayos contra sobrevoltajes de línea en el circuito de distribución que se muestra en la Figura n.° 1, que convierten las fases protegidas a líneas de tierra extras y así, entregan algunos beneficios incluso para las fases de transmisión no protegidas de más arriba.

Un cálculo inicial comparará los resultados con un valor fijo de resistencia a pie de tierra en cada torre, al incorporar una curva de voltio-tiempo, acoplamiento por impedancia de sobrevoltaje e inductancia de torre. Luego, se comparará el valor computado de la I_crit y la probabilidad de excederlo con un resultado compuesto según una distribución log-normal realista de la resistividad del suelo que cambia de torre a torre. Se demostrarán los efectos de corona por impulso en la I_crit para el circuito de transmisión con y sin la distribución construida bajo las líneas para mostrar la mejora en el acoplamiento. A los niveles de voltaje del sistema de transmisión y distribución asumidos (115 kV y 50 kV), el bias voltaje del sistema eléctrico no es tan importante, pero reduce levemente la I_crit, lo que aumenta la tasa de arco inverso en un factor de alrededor del 20 %, independiente de la impedancia a pie de tierra. La matriz de impedancia de sobrevoltaje se utiliza para determinar las corrientes que fluirán a través de cada pararrayos contra sobrevoltajes ubicado en paralelo con los aisladores del sistema de distribución. Según estas corrientes, se pueden restar las caídas de voltaje a través de los pararrayos de los voltajes en las fases protegidas para volver a evaluar los voltajes que aparecerán en las fases de transmisión sin protección.

Modelado Simplificado del Proceso de Arco Inverso en Excel

Selección de la Plataforma Apropiada para los Cálculos de Modelado
La versión de 1982 del EPRI Red Book Ch, 12 presenta un proceso paso a paso para calcular el desempeño de una línea de transmisión en condiciones de rayos. El IEEE modificó este algoritmo en una serie de lenguajes de programación computacional: FORTRAN, BASIC, C, Visual Basic for Applications y Python como una serie de programas FLASH. Hileman aportó un conjunto similar de programas BASIC para implementar el alcance del boletín técnico 63 del CIGRE para estimar el desempeño en condiciones de rayos. Recientemente, la Asociación de Normas del IEEE ha criticado la versión BASIC del programa FLASH en la Norma 1243^TM del IEEE porque no funciona directamente en Windows 10 ni en otros sistemas operativos modernos. La capacidad de ejecutar estos programas heredados se gestiona ahora con emuladores, pero se ha sugerido que los programas ejecutables, como el FLASH, deberían eliminarse de las normas futuras.

El EPRI ha enfrentado un dilema similar. Desarrolló una serie de “Applets”, que tienen como base el lenguaje Java, para respaldar estas revisiones de recursos de rayos y puestas a tierra en el periodo 2005-2010. Se esperaba que estos se mantuvieran independientes de los sistemas operativos y que se ejecutaran de manera exitosa en cualquier navegador web futuro. Desafortunadamente, el código fuente de las applets del EPRI es oculto para asegurar la integridad y la seguridad del programa y ahora, la mayor parte se han abandonado porque no se ejecutan en lo absoluto.

Aún existe la necesidad de ilustrar los conceptos técnicos y estadísticos de forma matemática. Microsoft Excel^TM parece ser el denominador común más bajo que se utiliza para este fin. Proporciona métodos adecuados para la manipulación de la matriz, la iteración y la simulación estadística para evaluar los cambios en el desempeño en condiciones de rayos que se esperaría cuando se agregan circuitos de distribución bajo los circuitos de transmisión, como se muestra en la Figura n.° 1.

Modelo de Arco Inverso según Tiempo de Rampa Fijo de 2 µs
Sucede que la opción original de una onda de rampa lineal con cero para un tiempo pico de 2 microsegundos (2 µs) sigue siendo una excelente opción para evaluar el sobrevoltaje que aparece a través de los aisladores en condiciones de sobrevoltaje por rayo. Por lo general, los primeros golpes de retorno negativos descendentes medidos tienen un frente cóncavo que alcanza su derivada máxima Smax, dI/dt justo en el pico de la onda de corriente. El tiempo de frente de rampa equivalente, al extrapolar hacia atrás a partir del pico en la tasa de Smax a corriente cero, parece aumentar lentamente en el rango de 1,8 a 2,5 µs, lo que depende de la magnitud pico de la corriente. En la Figura n.° 2 se fija el tiempo de aumento de cero a 100 % de 2 µs y se utiliza para convertir la inductancia de la torre en aumento de voltaje con el modelo ΔV = L dI/dt = LI/(2 µs). El aumento de voltaje en la parte superior de la torre es la suma del aumento de voltaje a pie de tierra Z_f ΔI y L dI/dt. El aumento de voltaje en las posiciones intermedias a lo largo de la torre se establece con el flujo de corriente y la inductancia desde ese punto a la tierra. A menudo, si la torre tiene una forma de cono, como un monopolo de acero, este se escala linealmente con la impedancia de sobrevoltaje constante desde el ápice.

Normalmente, los cálculos de arco inverso se realizan con los parámetros de primer golpe de retorno negativo, porque estos tienen los valores más grandes de I_pk que tienden a dar los niveles más altos de Vpk al usar lo indicado en la Figura n.° 2. No existe un valor único para I_pk, sino que este se describe mediante una distribución estadística de log-normal, con una media de 31 kA y una desviación estándar de ln(I_pk) entre 0,48 y 0,66.

La impedancia de pie a tierra de la torre golpeada Z_f depende del tamaño y la forma de la parte enterrada de la torre. Para un monopolo, como el que se muestra en la Figura n.° 1, es común que la profundidad de entierro se estime en al menos un 10 % del largo del poste más 0,6 m. Las alturas de los postes y las profundidades de entierro son relativamente constantes a lo largo de una sección de la línea. Sin embargo, la resistividad del suelo  (unidades de metros ohm o Ωm) también tiene una distribución log-normal. Se ha notado que la desviación estándar del logaritmo de resistividad, según una distancia de 300 m entre los lugares, está en un rango de 0,9 para las regiones en los Estados Unidos y Portugal. Esto significa que la distribución de Vpk, computada con los procesos que se muestran en la Figura n.° 2, es el producto de dos distribuciones estadísticas muy amplias, lo que significa que la falla siempre es una opción y nosotros estamos haciendo un diseño para lograr una especificación de tasa de falla deseada, tal como un disparo por 100 km de km de circuito por año.

Modelo de Arco Inverso con Distribución log-Normal de Impedancia a Pie de Tierra

En la Figura n.° 3 se utilizaron las funciones RAND() y LOGNORM.INV de Excel para ilustrar cómo las diferencias de poste a poste en la resistividad del suelo afectan el cálculo del desempeño en condiciones de rayos.

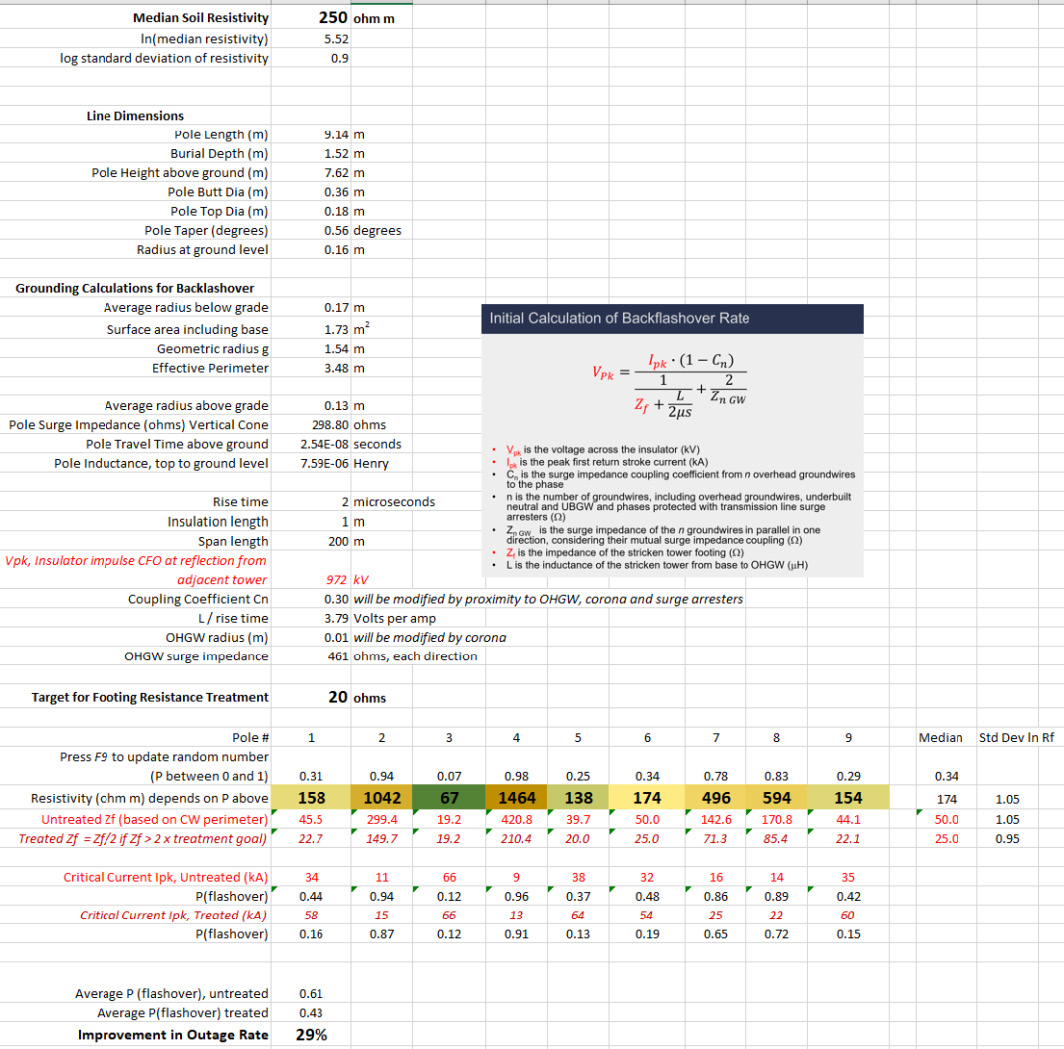
Se modelan nueve postes. A cada uno se le da un número RAND() al azar entre cero y 1. Luego, se utiliza esta probabilidad como un argumento en la función LOGNORM.INV (probabilidad, media, desviación estándar). En la primera fila de 250 Ωm se encuentra una resistividad del suelo media. Esta se convierte a la media de la distribución log-normal con LN(20) = 5,52. El valor de desviación estándar del logaritmo se fija en 0,9. Luego, las nueve celdas coloreadas, que se muestran en la Figura n.° 3, entregan los estimados de resistividad que varían de torre a torre, con un mínimo de 67 Ωm y un máximo de 1464 Ωm en esta simulación. Cada vez que se presiona la tecla F9, aparecen valores de probabilidad nuevos en cada celda y estos actualizan el resto de los cálculos.

El modelo que relaciona la impedancia a pie de torre Z_f con la resistividad ρ es simple, pero exacto. El radio geométrico de la parte del poste enterrada en el suelo se computa como g = 1,54 m, principalmente según la profundidad de entierro de 1,52 m. El área superficial de este cilindro levemente ahusado es A =1,73 m2. La expresión Z_f = ρ/(2πg) ln (11.8 g2/A) se invierte para dar un “perímetro eficaz”, el hemisferio equivalente, de P=3,48 m. Esto se utiliza en cada caso para convertir la resistividad en Z_f con un Z_f = ρ / P.

La inductancia del poste L se computa a partir de la impedancia de sobrevoltaje y el tiempo de recorrido a la velocidad de la luz. Así, la impedancia de sobrevoltaje de 299 Ω por el tiempo de recorrido de 0,254 µs da una inductancia L = _τZ = 7,6 µH. Cuando esto se divide por el tiempo de rampa de 2 µs, el aumento de voltaje relacionado con el poste se vuelve ΔV =7,6 µH / 2 µs = 3,8 voltios por amperio.

Más que computar el voltaje del aislador V_pk para un conjunto aleatorio de valores de I_pk, el cálculo que se muestra en la Figura n.° 3 manipula la expresión que se muestra en la Figura n.° 2 para dar la “corriente crítica” según un valor calculado de la resistencia al arco eléctrico del aislador. Se utiliza una curva voltio-tiempo para las cadenas de los aisladores cerámicos y se toma el tiempo de evaluación como el punto en el cual la onda de voltaje se vuelve no estándar, que es el tiempo que tarda la corriente en hacer el recorrido hacia atrás y adelante a las dos torres adyacentes.

Modelo de Arco Inverso con Distribución Log-Normal de Resistividad & Plan de Corrección

El modelo de log-normal de resistividad que se muestra en la Figura n.° 3 se puede utilizar para mostrar los efectos de un plan de corrección de conexión a tierra. A menudo, los gerentes de activos, que enfrentan un mal desempeño producto de los rayos, pondrán en marcha un proyecto para mejorar la resistencia de puesta a tierra en una línea. En un alcance no óptimo, la misma mejora, por ejemplo, varillas de accionamiento adicionales o contrapesos radiales enterrados, se instalarán en cada torre. Un alcance mejor fijaría un valor de impedancia objetivo, por ejemplo 20 Ω como se muestra en la Figura n.° 3. Se trataría cualquier estructura con Z_f > 20 Ω. Si se encuentra que Z_f está en el rango de 20 a 40 Ω, a menudo resulta práctico instalar suficientes electrodos a tierra nuevos dentro de 60 m del poste para lograr el valor objetivo. Sin embargo, para los casos de alta resistividad, por lo general, lo mejor que se puede lograr es una reducción del factor de dos. Así, por ejemplo, en el Poste 9, el valor inicial de Z_f = 44,1 Ω se reduce a 22,1 Ω, lo que significa una reducción significativa en la probabilidad de un arco eléctrico de 42 % a 15 %. Sin embargo, en el Poste 8, la reducción de 171 Ω a 85 Ω solo reduce la probabilidad de arco eléctrico desde un 89 % a un 72 %. Con una distribución log-normal típica de resistividad, la campaña de tierra fijada como objetivo se relacionaría con ocho de los nueve postes y se lograría una mejora del 30 % en la tasa de apagones por rayos.

Modelo de Arco Inverso con Pararrayos
Los pararrayos contra sobrevoltajes, ubicados a través de los aisladores, limitarán el sobrevoltaje local ya que pasan una fracción de corriente a los conductores de fase protegidos. Esto tiene la característica deseable de aumentar n, el número de líneas de tierra, como se muestra en la Figura n.° 2. También afectará al coeficiente de acoplamiento, que se fijó en C_n=0,3 (Figura n.° 3) para enfocarse en el rol de la resistividad del suelo con distribución log-normal. Siempre existe la pregunta de quién paga y quién se beneficia cuando se hace una inversión de capital. Cuando se consideran los pararrayos contra sobrevoltaje en los circuitos de distribución que se muestran en la Figura n.° 1, puede que un ingeniero de transmisión sea poco compasivo. Existirán arcos eléctricos a los circuitos de distribución, al poner sus fases en paralelo con la OHGW, incluso si no se han instalado pararrayos. Sin embargo, al entender el relativamente mal retorno de la inversión relacionada con las mejoras de tierra y las mejoras bien controladas logradas al hacer la misma inversión en pararrayos de voltaje medio, se puede conseguir algún reparto de costos equitativo.

Modelado de Acoplamiento Electromagnético en Línea de Cuatro Circuitos en Excel – Matriz de Acoplamiento por Impedancia de Sobrevoltaje

La mayor parte de los programas simplificados para computar el desempeño en condiciones de rayos tienen algunas limitantes con respecto al número de circuitos y líneas de tierra. A pesar de que solo hay una OHGW central única en la Figura n.° 1, aplicar un LSA a los seis conductores de la parte inferior los llevará al circuito de acoplamiento por impedancia de sobrevoltaje. Primero, esto se va a ilustrar con un modelo lineal. Luego, se explorarán los efectos del efecto corona por impulso en la matriz de impedancia de sobrevoltaje y acoplamiento. Finalmente, se evaluará el efecto de las caídas del voltaje de línea y de voltaje a través de los pararrayos.

Minitutorial: Matriz de Impedancia de Sobrevoltaje Propia & Mutua

La impedancia de un conductor sobre la tierra a una frecuencia industrial es un número complejo, pero a medida que la frecuencia f aumenta de 50-60 Hz a sobre los 100 kHz, el término de resistencia en serie se vuelve insignificante comparado con la reactancia inductiva. La impedancia de sobrevoltaje de un cable según la inductancia L y la capacitancia C por longitud de unidad, converge a un valor escalar:

La impedancia de sobrevoltaje Z₁₁en la Ecuación 1 tiene unidades de ohm. Los dobles subíndices indican que es la impedancia de sobrevoltaje propia del conductor 1 con radio r₁. Si existe otro conductor 2 cerca, entonces habrá una “impedancia de sobrevoltaje mutua” Z₁₂ a partir de la Ecuación 2 que será igual a Z₂₁.

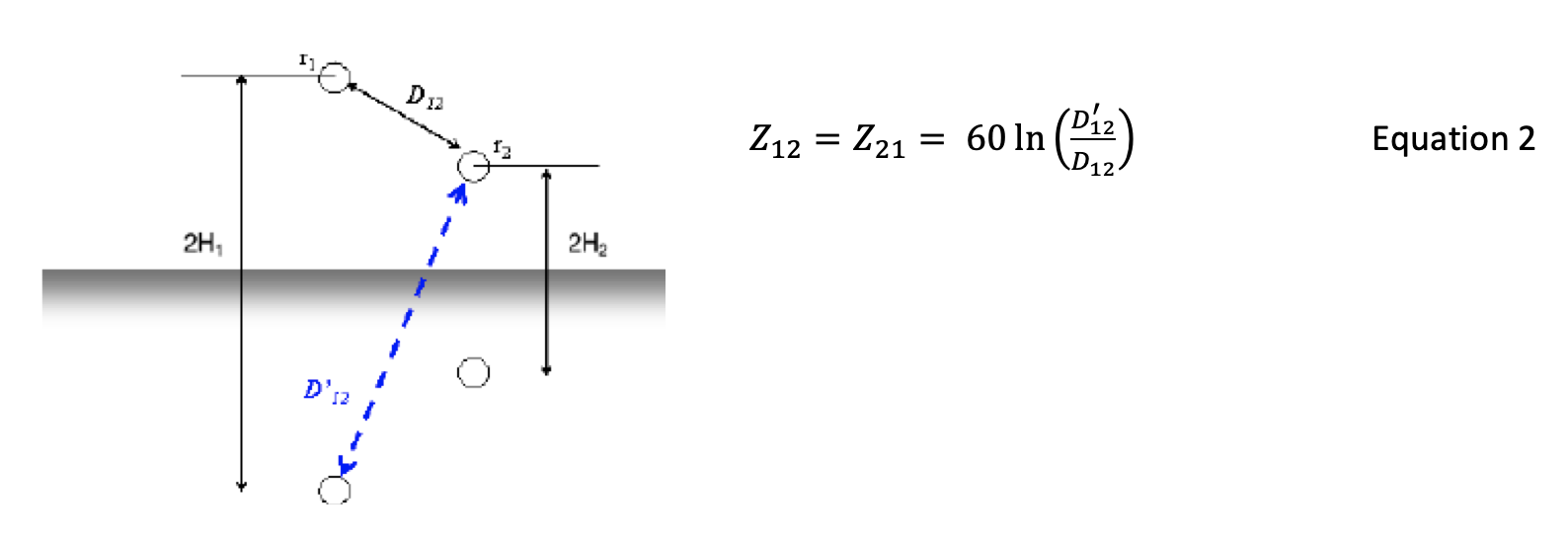Si se aplica un impulso de voltaje al conductor 1, fluirá la corriente de V­₁ / Z₁₁.Una fracción de este voltaje,C₂ V₁ aparecerá en el conductor 2, incluso si se aísla y no fluye corriente en él. Se puede construir una matriz de valores de impedancia de sobrevoltaje a partir de las posiciones del conductor y los radios del conductor. Los cálculos que se muestran en la Figura n.° 4 incluyen la altura de los conductores en la torre y las alturas promedio a lo largo de las retenidas aéreas, dadas por las alturas en la torre menos 2/3 de las caídas.

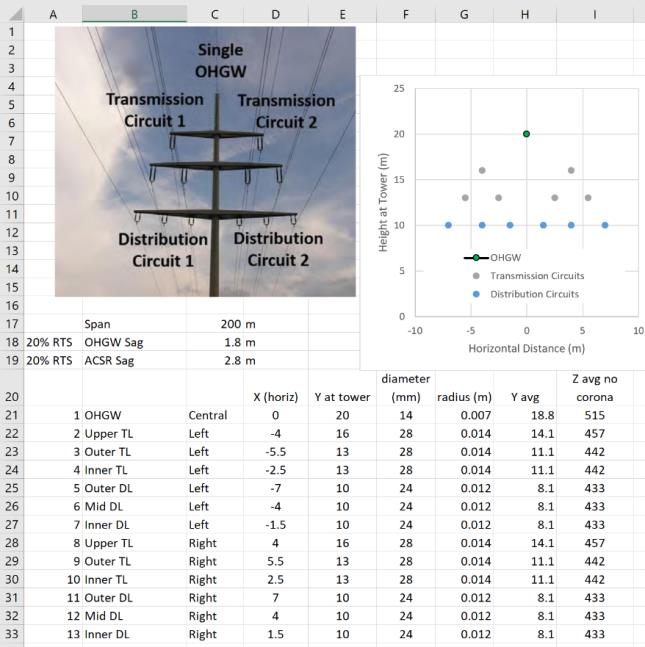
Se asume que las tensiones diarias de los circuitos de transmisión y distribución son las mismas, 20 % de la resistencia a la tensión nominal de los conductores. Esto es típico para las líneas de transmisión y es probable que se utilice la misma tensión para los conductores de línea de distribución de más abajo, de manera que las caídas coincidan. Las dimensiones que se muestran en la Figura n.° 4 se utilizan junto con las referencias de celda parciales, tales como C$36 y $B37 en la celda C37 para hacer el cálculo según las dimensiones en la fila 36 C-O y en la columna B de las filas 37-49. La primera matriz es la separación horizontal, la segunda matriz es la separación vertical para D12 y la tercera matriz, que se muestra en la Figura n.° 5, es la distancia vertical al conductor imagen para D’₁₂.

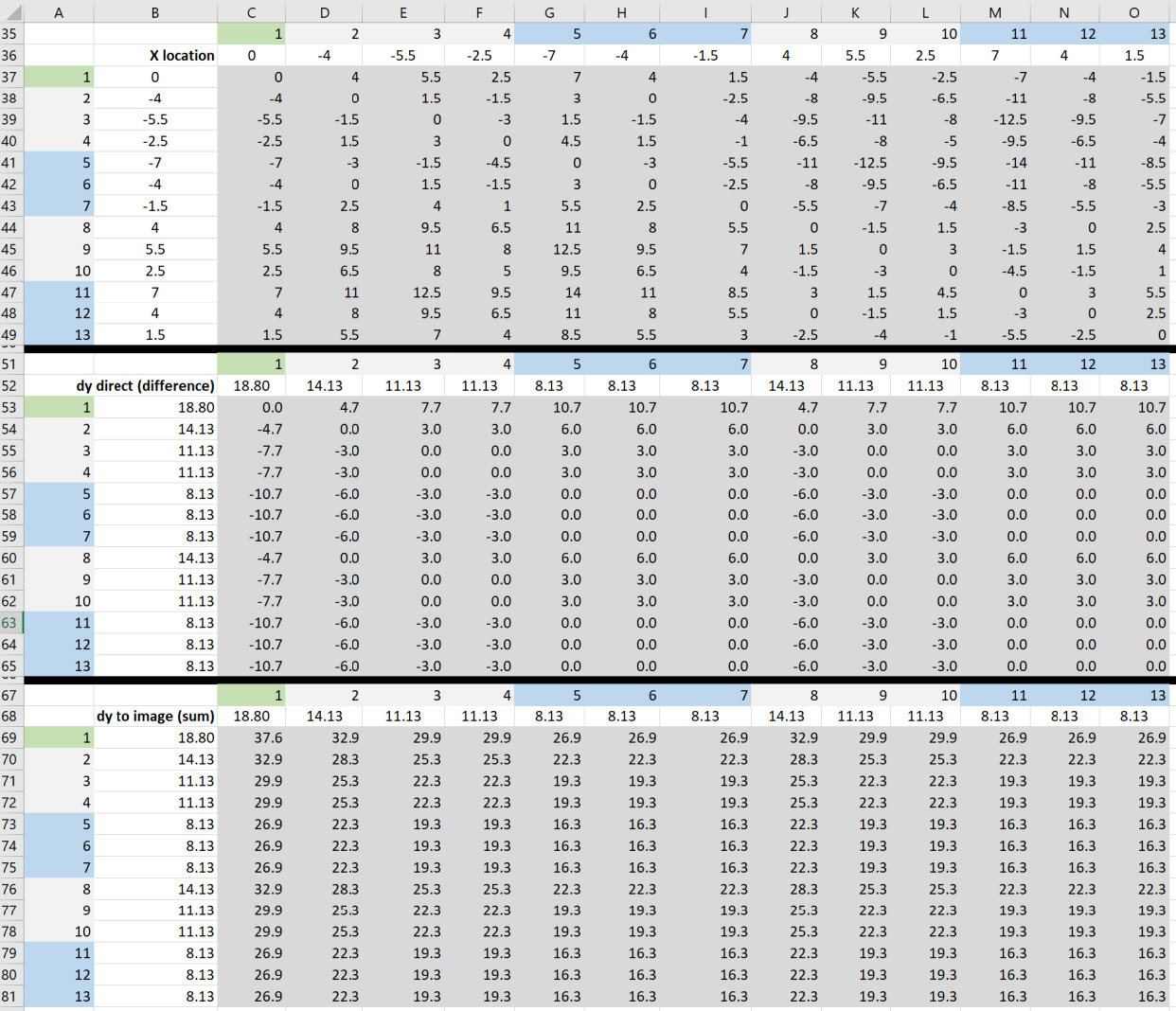
Una vez que se han formado las distancia entre los conductores, se utilizan la Ecuación 1 y la Ecuación 2 para computar una matriz de impedancia de sobrevoltaje como se muestra en la Figura n.° 6.

Minitutorial: Matemática de Matriz en Excel

Microsoft Excel tiene funciones de matriz incorporadas: MMULT y MINVERSE. Una búsqueda en línea puede entregar estrategias para invertir en matrices complejas, pero para los cálculos de rayo, estas no son necesarias. La matriz cuadrada [Z_ij] que se muestra en la Figura n.° 6 se puede multiplicar por un vector de corrientes [I_i] para producir un vector de voltajes [V_i]. Eventualmente, los archivos de ayuda de Excel revelan que la manera de ver todos los voltajes de una multiplicación de matriz es configurar [Z], por ejemplo, en las celdas C117-O129, luego, configurar el vector de corrientes [I] cerca en las celdas Q117-O129, luego:
• Destaque todas las celdas donde aparecerán los valores de voltaje, tal vez S117:S129

• Escriba “ = MMULT(C117:O129,Q117:Q129) ” sin las comillas.

• Presione F2, luego presione (todo junto de una vez) CTRL, Shift y Enter
Esto hará que se escriban llaves {=MMULT(C117:O129,Q117:Q129)} y aparecerán los trece voltajes en el área designada.

El mismo proceso funciona con la función MINVERSE si quiere invertir la matriz de impedancia y multiplicarla por un vector de voltajes para obtener un vector de corrientes en cada conductor. Sin embargo, no es correcto asumir que las corrientes en las fases accionadas serán todas iguales.

Coeficientes de Acoplamiento para OHGW Única

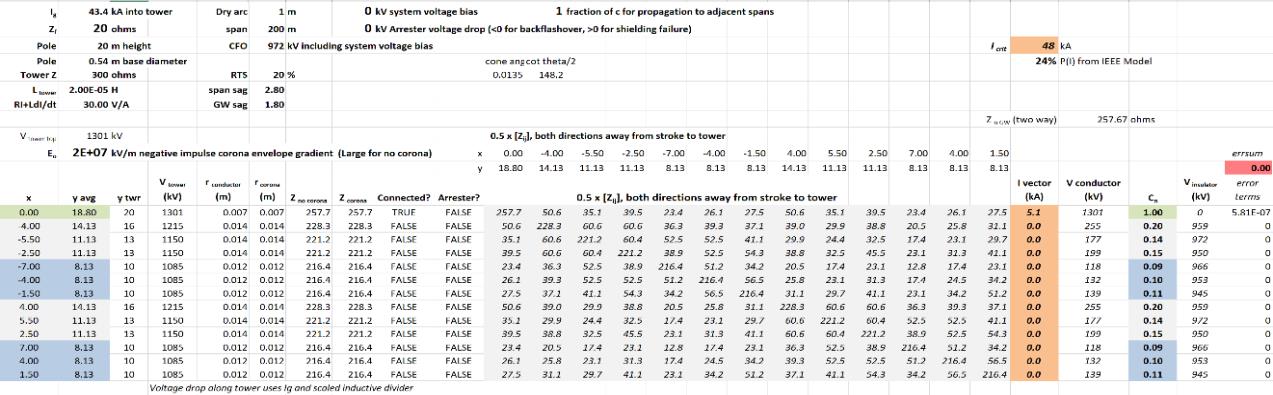
En la Figura n.° 7 se implementa la multiplicación de una matriz de impedancia de sobrevoltaje para la línea de la Figura n.° 4 por un vector de corrientes con 1 A impreso en la OHGW (conductor 1, verde sombreado). Los otros doce conductores están aislados y no tienen corriente. El aumento de voltaje en la OHGW es, como se espera, 515 V de su impedancia de sobrevoltaje Z₁₁. Lo que es más difícil de visualizar es que los voltajes entre 47 y 101 V aparecen en todos los otros conductores debido a la impedancia de sobrevoltaje mutua.

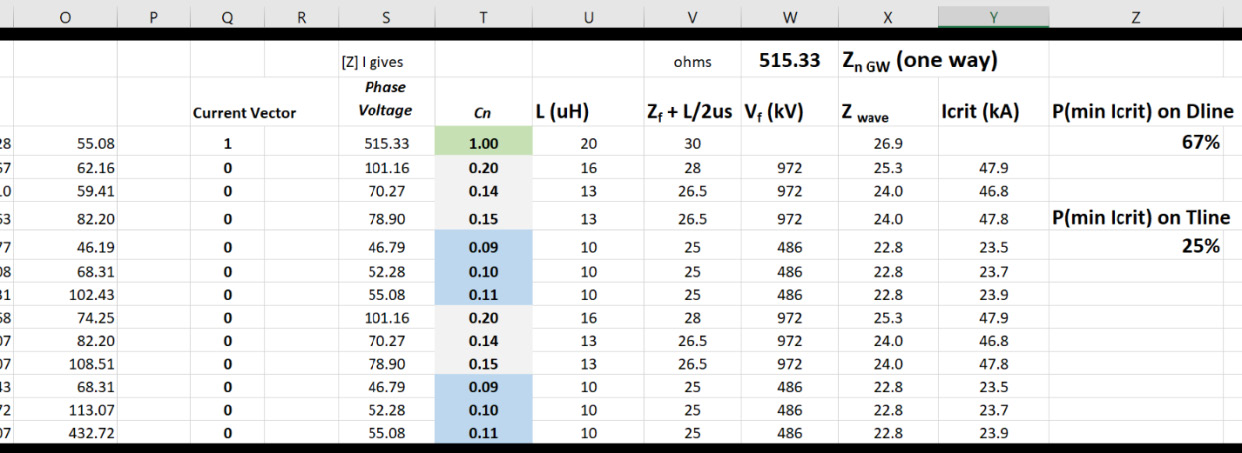
Los coeficientes de acoplamiento C_n se utilizan en una implementación del cálculo de la Figura n.° 2 para cada una de las fases. El voltaje de arco eléctrico computado para el aislador de 115 kV con una distancia de arco en seco de 1 m, con longitud de las retenidas aéreas de 200 m, es 972 kV y el voltaje de arco eléctrico para el circuito de distribución es la mitad de eso, 486 kV. La columna etiquetada Z_wave en la Figura n.° 7 es el inverso del denominador de la Figura n.° 2. Las corrientes críticas para cada fase en la columna siguiente se computan a partir de la resistencia de aislación, dividida por Z_wave y corregidas para el acoplamiento al dividirlas por (1-C_n).

La corriente crítica mínima en este cálculo, con Z_f = 20 Ω, es 23,5 kA y la probabilidad de exceder esta corriente es de alrededor de un 67 %. Así, dos de cada tres destellos de rayo causarán al menos un arco eléctrico en un circuito de distribución. Las corrientes críticas más bajas en los circuitos de transmisión se computan para los conductores 3 y 9, que son las fases más exteriores. Se computa que la probabilidad de exceder los 46,8 kA es del 25 %. Este es el desempeño esperado para una línea de transmisión que tenía las mismas dimensiones, pero sin distribución construida bajo las líneas.

Estos resultados nos dejan una lección importante. La línea de distribución tiene un mal desempeño en condiciones de rayos, incluso aunque tenga protección de línea de tierra aérea porque su aislación de 0,5 m es relativamente débil. La línea de 115 kV con 1 m de aislación tendría una tasa de apagón que es 2,7 veces más baja. Esto se ofrece como una razón de por qué la mayor parte de los circuitos de transmisión están apantallados, mientras que la mayor parte de los circuitos de distribución no.

Coeficientes de Acoplamiento para Pararrayos en Todos los Aisladores de Distribución

No es caro comprar pararrayos contra sobrevoltajes para los sistemas de distribución. Hoy en día, la mayor parte de los productos ofrece un historial sólido del desempeño eléctrico confiable. Más que instalar aisladores de 1 m en las fases del sistema de distribución, consideramos proteger cada aislador de 0,5 m con su propio pararrayos contra sobrevoltaje.

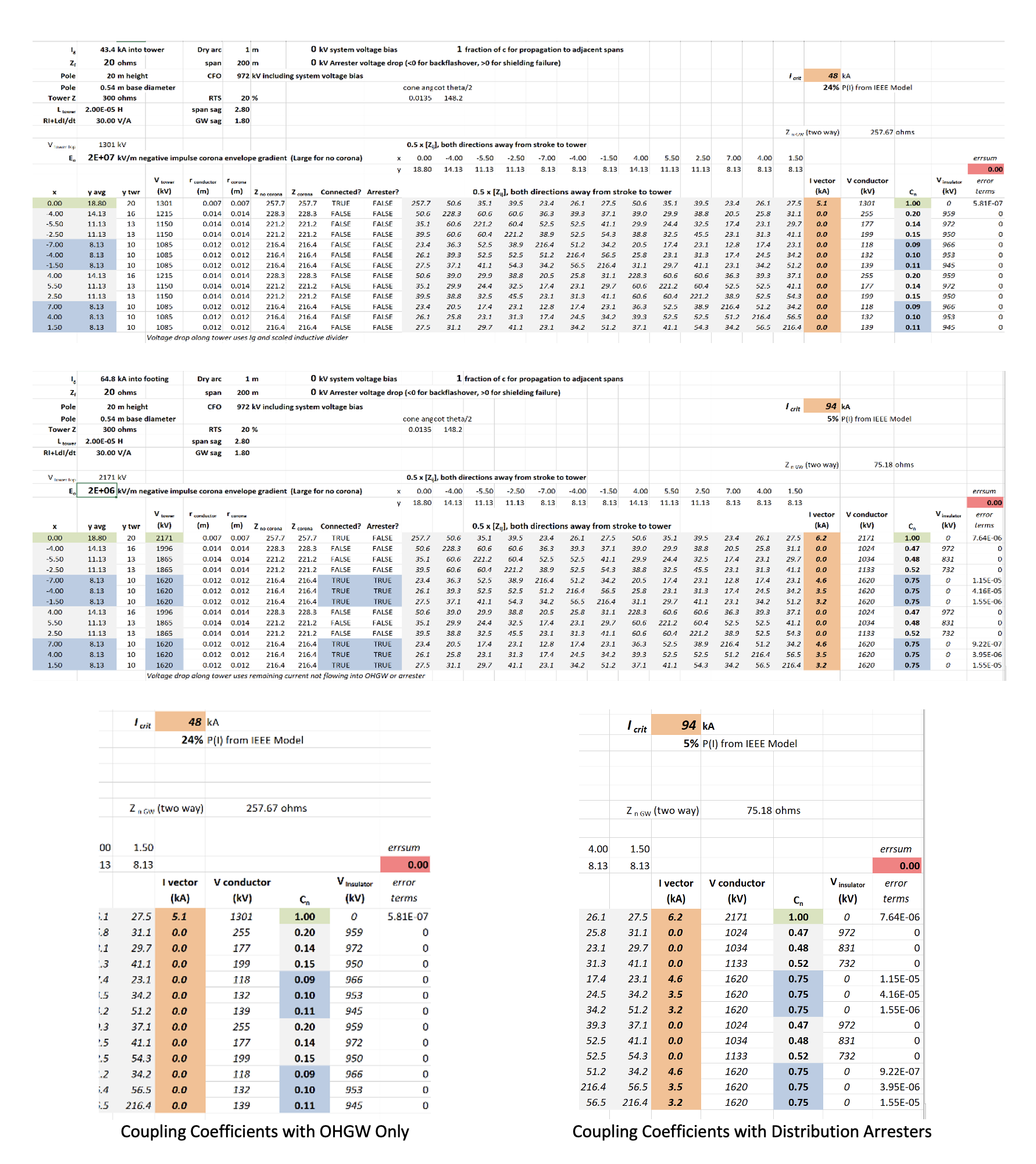
Se puede hacer un estimado rápido de los cambios en el coeficiente de acoplamiento y de los aumentos en la corriente crítica al alterar el vector de corriente de la Figura n.° 7 para que tenga corrientes de unidad en cada fase protegida. Los elementos de la hoja de cálculo que se muestran desde la Figura n.° 4 a la 7, se muestran compactados en la Figura n.° 8. Los coeficientes de acoplamiento y las corrientes críticas coinciden para la configuración de la OHGW única. Luego, el vector de las corrientes se ajusta en la Figura n.° 8, de manera que las corrientes también fluyan a cada uno de los seis conductores de fase del sistema de distribución.

Cada valor de matriz de impedancia de sobrevoltaje que se muestra en la Figura n.° 8 es exactamente la mitad de los valores que se muestran en la Figura n.° 6. En la consolidación, las fórmulas implementaron el hecho que corrientes iguales fluyen en dos direcciones desde la torre a cualquier OHGW o conductor que se haya protegido con un LSA. Además, los voltajes que aparecen en la varilla cruzada de la parte inferior en la Figura n.° 1, destacadas con azul en la Figura n.° 8, son más bajos que el voltaje en la parte superior de la torre, destacado en verde, porque la inductancia desde la varilla cruzada inferior a la tierra es más baja.

En la Figura n.° 8 se muestra que el valor de I_crit para los circuitos de transmisión aumenta de 48 a 94 kA cuando se instalan los pararrayos ideales en las seis fases de los dos circuitos de distribución. Esto daría un factor de mejora cinco en la tasa de apagones por rayos, según el cambio en la probabilidad de 24 % hasta 5 %. Esto se compara favorablemente con las mismas campañas de mejora de tierra en términos de capital y costos de mantenimiento, así como de eficacia a largo plazo.

Más Mejoras en el Acoplamiento: Efecto Corona de Impulso

En condiciones de operación comunes, los ingenieros de voltaje alto entienden que los campos eléctricos locales altos pueden causar descargas parciales, tales como el efecto corona. El efecto corona puede ser benigno, por ejemplo, una marca ultravioleta en el extremo de una chaveta con pasador en la tapa de un aislador. En algunas condiciones, como durante una fuerte lluvia, el efecto corona puede ser intenso con ruido audible distintivo, así como con radiación electromagnética de banda ancha desde los espacios libres entre un conductor y una antena. El efecto corona puede ser un indicador de un daño en curso en los aisladores. Las tecnologías de cámaras ultravioleta solares ciegas a veces pueden distinguir una fuente de efecto corona. Generalmente, las líneas no deberían presentar efecto corona en condiciones limpias y secas. Así, las cámaras UV son una herramienta importante para inspeccionar la línea.

En condiciones de sobrevoltaje por rayo, el efecto corona pasa de ser un “enemigo” a ser un “amigo”. Los voltajes altos que se computaron con el modelo de la Figura n.° 2 hacen que se formen envolventes de corona alrededor de las torres y los conductores. Estas tienen tres efectos principales:

• El efecto corona genera un aumento en la capacitancia a tierra, que reduce la impedancia de sobrevoltaje paralela Zn GW de cualquier línea de tierra aérea y cualquier fase protegida con pararrayos.

• El efecto corona causa un aumento en los coeficientes de acoplamiento de los conductores accionados (OHGW o fase de distribución protegida con pararrayos) y no accionados (fase de transmisión sin protección).

• El efecto corona (en la forma de ionización de suelo) puede reducir las impedancias a pie de tierra Z_f para las corrientes grandes.

El cuarto efecto de enlentecer de manera efectiva la velocidad de propagación a las retenidas aéreas adyacentes no es útil y se discute por separado.

Una de las diferencias más interesantes entre la práctica del IEEE y el CIGRE es el tratamiento del efecto corona. El IEEE incluye el efecto corona en las líneas aéreas con un modelo simplificado y lo ignora bastante al evaluar la impedancia a pie de tierra, ya que usa la lógica que las corrientes requeridas para hacer una ionización sustancial del suelo son demasiado grandes para ser relevantes para el cálculo del arco inverso. Por el contrario, el CIGRE hace que los efectos corona en las OHGW sean difíciles de modelar en los programas de transiente electromagnético, pero la TB 63 sí incluye un modelo simple para la ionización del suelo.

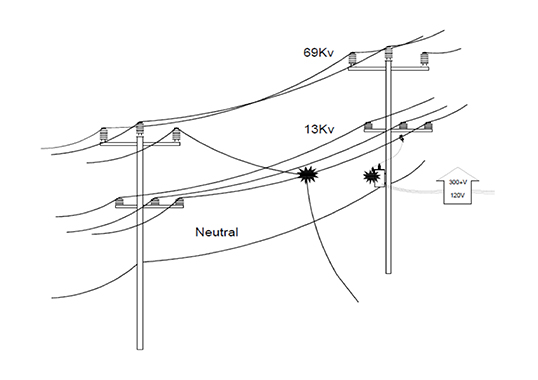
Comenzamos con una gradiente en el borde de la envolvente de corona, E_o y esta se fijó en E_o =1500 kV/m para la polaridad negativa. Luego, el radio del efecto corona R_c (m) es dado por:

Donde h es la altura promedio sobre el suelo (m) y V es el voltaje aplicado. Si R_c es menos que los radios físicos del conductor, no hay efecto corona ni cambio en la matriz de impedancia de sobrevoltaje. La ecuación 3 es ‘repetitiva’, que es el valor de R_c que aparece en ambos lados del signo igual. Sin embargo, tiene una característica interesante que la hace fácil de usar en el modelo Excel. El valor de R_c converge rápidamente. Se puede utilizar cualquier punto de partida inicial, por ejemplo, R_c = 1 m. Luego, una celda adyacente computa un valor nuevo de R_c. Después de hacer cinco cálculos, cada vez con un valor de R_c nuevo, se obtiene el valor final. Esto es esencialmente una solución de forma cerrada y la función MAX(R_c, r_conductor) finalizará el modelo de manera que los eventos de corriente baja no causen un efecto corona, pero los eventos de gran corriente, sí.

La envolvente de corona solo modifica el término capacitancia en la expresión de impedancia de sobrevoltaje. Esto significa que la impedancia de sobrevoltaje propia en condiciones de efecto corona será:

El acoplamiento modificado por el efecto corona se deshabilitó en los cálculos de la Figura n.° 8 al fijar E_o en un valor grande, 2E+06. Esto aseguró que R_c fuera menor que r_conductor, y el valor más grande de los dos se utilizó para computar Z_Corona. Cuando se sustituye el valor recomendado de E_o = 1500 kV/m para polaridad negativa en la Figura n.° 9, se muestra que la corriente crítica aumenta de 94 kA a 120 kA, principalmente porque los coeficientes de acoplamiento para el circuito de transmisión aumentan de 0,47 ≤ C_n ≤ 0,52 a 0,55 ≤ C_n ≤ 0,60. También existe una reducción modesta en Z_{n GW} de 75 Ω a 65 Ω.

Influencia del Voltaje de Línea Instantáneo de un Circuito de Transmisión

Los rayos tienden a tener polaridad negativa en la mayor parte de las regiones casi todo el año. En la Figura n.° 10 se muestra que el voltaje del sistema eléctrico de ac instantáneo puede ser positivo o negativo, lo que depende de la fase y del ángulo de fase. Al menos una de las fases tendrá un voltaje positivo, que se agregará a la tensión en el aislador en condiciones de rayos. Como referencia, la duración típica de un rayo de 100 µs corresponde a un poco más que 2° a 60 Hz, como se muestra en la Figura n.° 10.

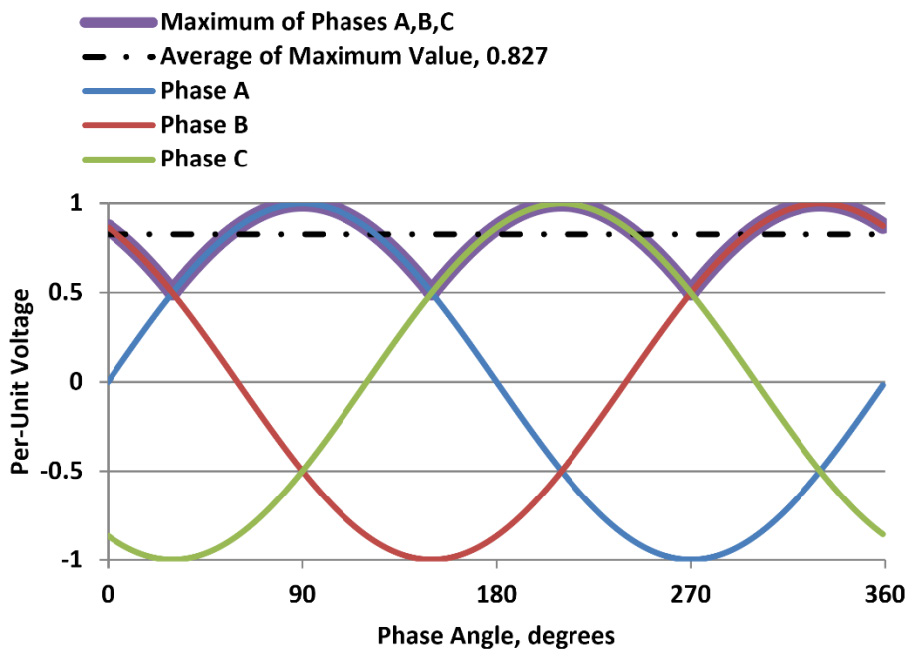
El máximo de las fases A, B y C, promediado en el periodo completo de 360°, da un valor de 0,827 por unidad (pu), donde 1 pu es el máximo del voltaje de línea a tierra (como se muestra). Más que hacer los cálculos para cada valor del ángulo de fase, se puede tratar la influencia del voltaje del sistema solo con restar 0,827 pu del voltaje crítico del arco eléctrico.

El CFO que se muestra en la Figura n.° 9 fue de 972 kV. Cuando el bias voltaje de un sistema de transmisión de 115 kV se incluye en la Figura n.° 11, el CFO se reduce eficazmente en 0,827 • √2 • (115 kV)/ √3 a 895 kV. Con una mayor tensión a través de los aisladores, esperamos que la corriente crítica descienda y lo hace: cae desde I_crit=120 kA a I_crit=109 kA, como se muestra en la Figura n.° 11.

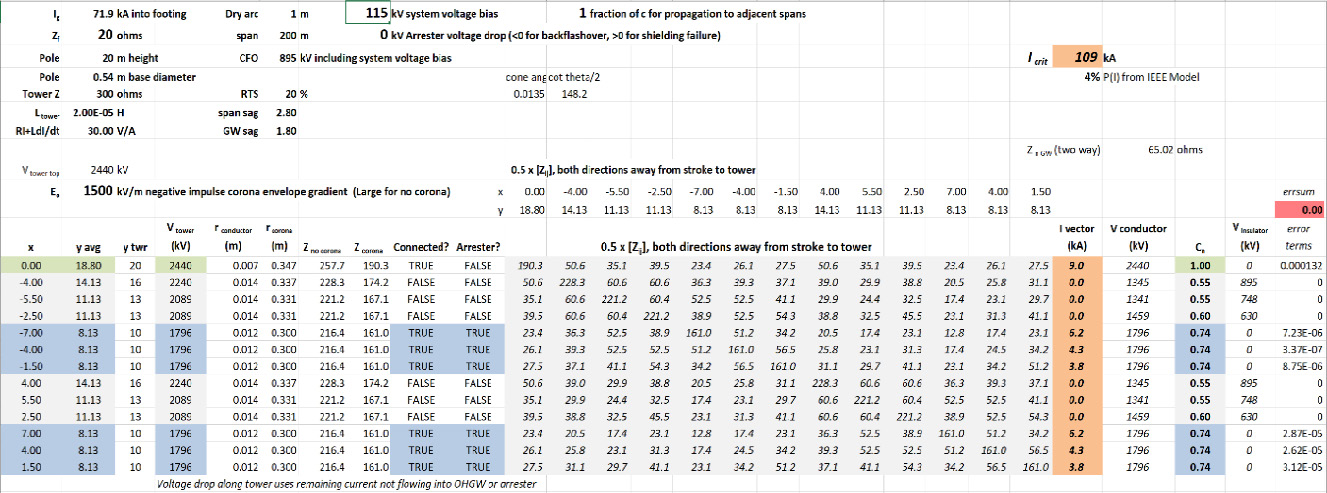
La probabilidad de exceder la I_crit = 109 kA con el bias voltaje del sistema ac aún bajo es de un 4 %, como se muestra en la Figura n.° 11,comparado con el 3 % sin voltaje de línea, como se muestra en la Figura n.° 10. Este buen desempeño se relaciona con el valor bajo de Z_f = 20 Ω junto con los beneficios de los seis pararrayos en los circuitos de distribución, lo que da coeficientes de acoplamiento de 0,55 a 0,6 en las fases de transmisión que no se cambian de los cálculos anteriores y se usa el mismo E_o = 1500 kV/m para la gradiente de envolvente de corona.

Influencia de la Velocidad de Propagación Modificada por el Efecto Corona

El valor del voltaje del aislador V_Pk que se utiliza en la Figura n.° 2 para computar la I_crit se basa en la distancia de arco seco del aislador y el tiempo de la descarga disruptiva. Por lo general, para los aisladores de porcelana, la resistencia se evalúa con un tiempo de arco eléctrico de 2 µs, a una gradiente de 822 kV por metro, más que con la gradiente de arco eléctrico por impulso de rayo de 520 a 560 kV por metro. El tiempo que se utilizó en el ajuste de la curva de voltio-tiempo se considera el tiempo que tardan las reflexiones de cancelación en retornar desde las dos estructuras adyacentes. Este tiempo de recorrido bidireccional es una función de la longitud de las retenidas aéreas y puede ser tan corto como 0,7 µs para retenidas aéreas de 100 m o de hasta 2,7 µs para retenidas aéreas de 400 m.

Las pruebas donde se aplicaron impulsos de rayo a conductores establecieron que existe un aumento continuo en el tiempo de aumento observado para la parte del voltaje sobre el umbral del efecto corona. Este efecto, que se puede tratar al asumir la velocidad de propagación, es, de algún modo, menor a la velocidad de la luz. El retardo retiene la tensión en los aisladores de la torre golpeada por un mayor tiempo. La velocidad de propagación se ajustó, como se muestra en la Figura n.° 12, al 90 % de la velocidad de la luz (0.9 c).

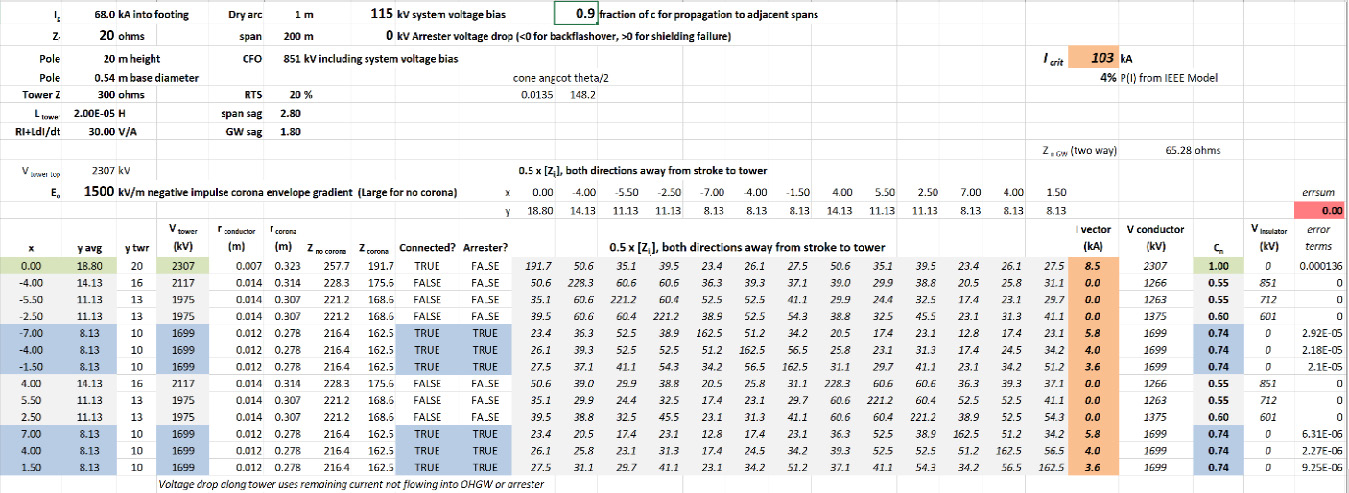
El bias voltaje del sistema que incluye CFO y que se muestra en la Figura n.° 12, al compararlo con la Figura n.° 11, cae de 895 kV a 951 kV. La corriente crítica cae de I_crit = 109 kA, como se muestra en la Figura n.° 11, a I_crit = 103 kA, como se muestra en la Figura n.° 12, pero el efecto sobre la probabilidad de exceder la I_crit es mínimo, manteniéndose en un 4 % para ambos casos.

Influencia de la Caída de Voltaje del Pararrayos contra Sobrevoltaje

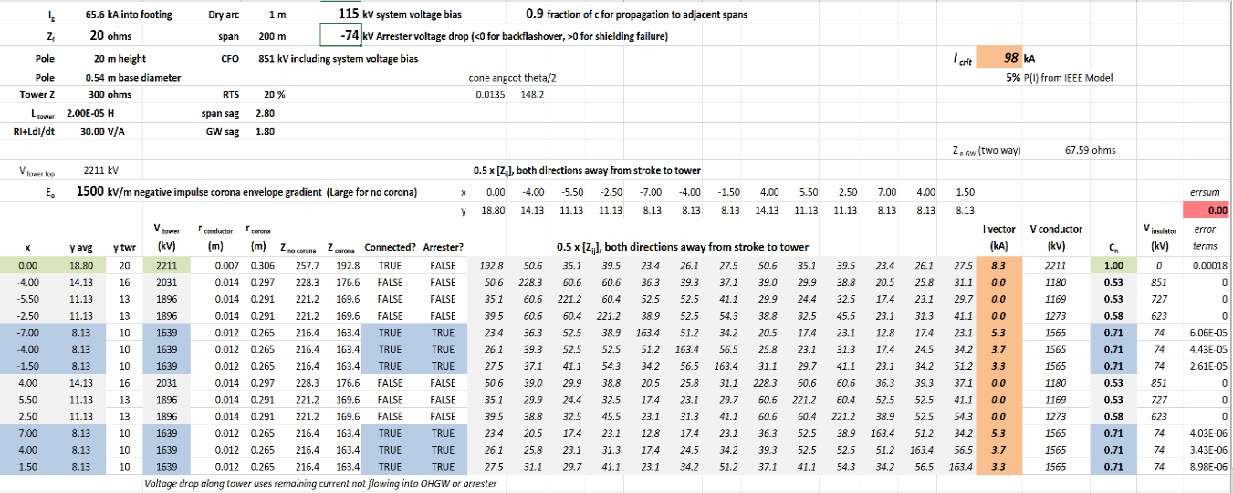
Los vectores de solución que se muestran en las Figuras n.° 9, 11 & 12 sugieren que una corriente en el rango de 4 a 7 kA fluirá a cada LSA del circuito de distribución. Habrá una caída de voltaje que se relaciona con este flujo de corriente que se debería restar de los voltajes que aparecen en cada fase. Un LSA MCOV de 33 kV típico tiene un voltaje de alrededor de 74 kV con corriente de 5 kA, aumenta a 87 kV a 10 kA y a 101 kV a 20 kA. Se ingresó la caída de voltaje en la celda destacada que se muestra en la Figura n.° 13.

Para esta situación, la caída de voltaje a través de los pararrayos de línea del sistema de distribución reduce los voltajes que aparecerán en estas fases de 1699 kV, como se muestra en la Figura n.° 12, a 1565 kV, como se muestra en la Figura n.° 13. Se producen las reducciones correspondientes en las corrientes que fluyen a cada fase de distribución de protección y en los valores de coeficiente de acoplamiento C_n para los circuitos de transmisión. El efecto general es un valor reducido de I_crit = 98 kA y una probabilidad del 5% de exceder este.

Una referencia a lo que se muestra en la Figura n.° 8 confirma que el estimado original de la I_crit, al ignorar los beneficios del acoplamiento modificado por el efecto corona, el bias voltaje de línea, la lenta velocidad de propagación con efecto corona y el efecto de la caída del voltaje del pararrayos, dio alrededor del mismo valor de I_crit = 94 kA en este caso. Hay algo que vale la pena revisar en cualquier evaluación simple o detallada del proceso de arco inverso.

Efecto de la Impedancia a Pie de Tierra Z_f en los Resultados

Más arriba, se ha enfatizado que la variación de Z_f de torre a torre es aleatoria y se rige por la distribución log-normal. La impedancia a pie de tierra de corriente baja varió de 19 a 421 Ω en una simulación típica de nueve torres, como se muestra en la Figura n.° 3. Para terminar la sección del modelado del proceso de arco inverso, el modelo simplificado (sin efectos corona, sin bias voltaje del sistema, sin caída de voltaje del pararrayos) se comparará con la evaluación, al seguir lo que se indica en la Figura n.° 13 con todos estos factores.

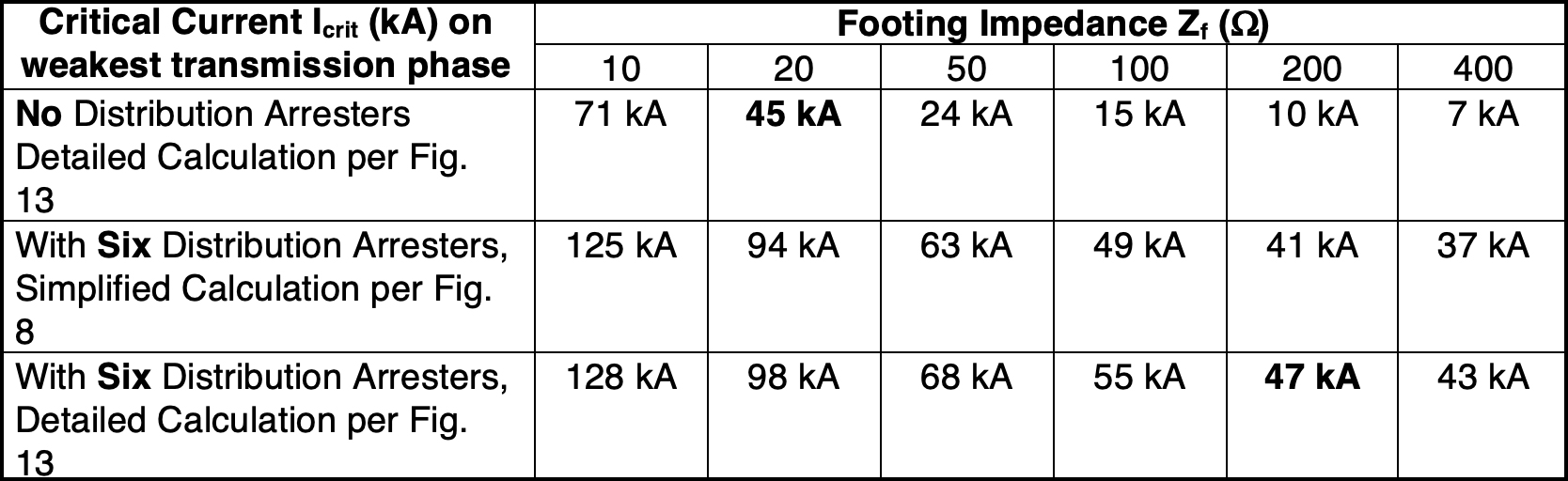
Una línea construida con pararrayos y una impedancia a pie de tierra de 200 Ω tendría el mismo desempeño que una línea con impedancia a pie de tierra de 20 Ω y sin pararrayos en el circuito de distribución construido bajo la línea, según los valores similares de I_crit que se muestran en la Tabla 1.

La industria está en el proceso de decidir si los efectos de la ionización del suelo o la dependencia de la frecuencia de la resistividad del suelo ofrece la mejor explicación para el desempeño de las líneas de transmisión con una impedancia a pie de torre alta. Ambos efectos reducen la Z_f de un valor de frecuencia baja, corriente baja medido. Para una simulación como se muestra en la Figura n.° 3 con ρ=250 Ωm, el modelo de ionización de Korsuncev sugiere que la interfaz del monopolo pequeño al suelo comenzará a ionizar a una corriente bastante por debajo de nuestro nivel de I_crit anticipado, de manera que la Z_f para 30 kA puede ser menor a la mitad de los valores de corriente baja. Al contrario de este modelo, que es muy difícil de respaldar con pruebas, los efectos de la resistividad dependiente de la frecuencia se pueden y se tienen que verificar en muchos estudios de campo prácticos, como se describe en el documento del CIGRE Working Group C4.33. Un tema final es una combinación de ambos efectos: se anticipa que la envolvente de corona de ionización en el suelo soportará una gradiente mayor de hasta 1500 kV/m en un suelo denso y rocoso, comparado con los 400 kV/m en un suelo de resistividad baja.

Aspectos Mecánicos de los Pararrayos de Distribución Construidos bajo la Línea

Los aisladores que se muestran en la Figura n.° 1 limitan algunos movimientos horizontales de los conductores, lo que los hace, según la definición del EPRI-USA, de un diseño “compacto”. Los aisladores rígidos o semirrígidos reducen la posibilidad de contactos de conductor a conductor. Estos también simplifican la instalación de pararrayos contra sobrevoltajes de línea (LSA) en paralelo para limitar los sobrevoltajes por rayos y evitar los arcos eléctricos.

Por ejemplo, el concepto de pararrayos de línea sin entrehierro (NGLA) de los años 90 de Hydro-Québec, que se muestra en la Figura n.° 14, muestra una placa metálica de soporte apernada entre el aislador no cerámico de pedestal, el poste y el soporte del conductor. Un pararrayos MCOV de 39 kV de nominación adecuada cuelga del extremo de esta placa. En la parte inferior del pararrayos existe un conductor a tierra de cobre AWG 4 flexible, también de unos 750 mm de largo, unido a un módulo de desconexión explosivo en la parte inferior del pararrayos. El montaje rígido por encima y la corta longitud del conductor por debajo mitigan muchos problemas como la flexión, la vibración y la fatiga.

Desde fines de la década de los 90, cuando se exploró este concepto de pararrayo de sistema de subtransmisión, los LSA se han desarrollado aún más y se han aplicado de manera exitosa en muchas líneas de transmisión. El término “TLSA” se ha reservado para los voltajes a nivel de transmisión que, por lo general, son líneas apantalladas con voltaje de fase a fase de al menos 69 kV. La configuración mecánica que se sugiere en la Figura n.° 14 se ha (exitosamente):

● rotado 90°, de manera que el pararrayos cuelgue por debajo de un aislador de poste horizontal,

● invertido, de manera que un brazo pescante soporte un TLSA desde abajo y

● duplicado con brazos de soporte en cada extremo de un aislador, dos TLSA y un intervalo de aire en serie entre ellos para formar un pararrayos de línea con entrehierro externo (EGLA).

Un acercamiento a la bien conocida aplicación de TLSA de 400 kV en unas pocas retenidas aéreas en Noruega muestra una cinta metálica similar, semirrígida que mantiene el extremo superior del cuerpo del pararrayos alejado de la cabeza del aislador de poste. El brazo de soporte del TLSA de 400 kV, que se muestra en la Figura n.° 15, está ubicado entre los conductores de fase gemelos en una zona equipotencial que puede eliminar los problemas con el efecto corona alrededor de los elementos de radio pequeño.

Los pernos de conexión en la cabeza del pararrayos se apantallan aún más con un par de anillos anticorona.

Además del apantallamiento de las piezas mecánicas con anillos anticorona, los proyectos para aplicar TLSA tienen que considerar la tensión del conductor. Muchos circuitos de líneas de transmisión se diseñan con tensiones máximas del orden del 20 % de la resistencia a la tensión nominal (RTS) del conductor, donde los ingenieros de sistemas de distribución están más familiarizados con líneas que tienen cadenas a RTS de 5-10 %. Las tensiones más altas pueden llevar a posibles problemas con la vibración eólica. El CIGRE ha discutido la interacción de los TLSA con los amortiguadores de vibración como un problema de aplicación. Una característica prevista de las disposiciones de montaje que se muestran en las Figuras n.° 14 y 15 es que el montaje de los pararrayos no interfiere con los amortiguadores de vibración. En la Figura n.° 15 los doce amortiguadores de vibración eólica son los pares de pesos, conectados con un cable y montados a una corta distancia entre sí en cada lado de las abrazaderas del conductor.

Relación con Contactos de Circuito Cruzado
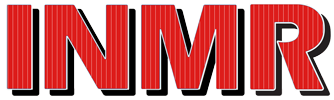
INMR ha presentado varios artículos que describen un concepto, que se originó en Dominion Virginia Power y que también se adoptó en Fortis BC, que utiliza pararrayos en un circuito de distribución como protección contra las fallas por circuito cruzado. El esquema que se muestra en la Figura n.° 16 muestra el problema de un conductor roto en una línea de 69 kV no apantallada que contacta la fase de 13 kV de más abajo. Esto generará sobrevoltajes sustanciales e inesperados que pueden ser de larga duración si los relés no reconocen la condición inusual rápidamente.

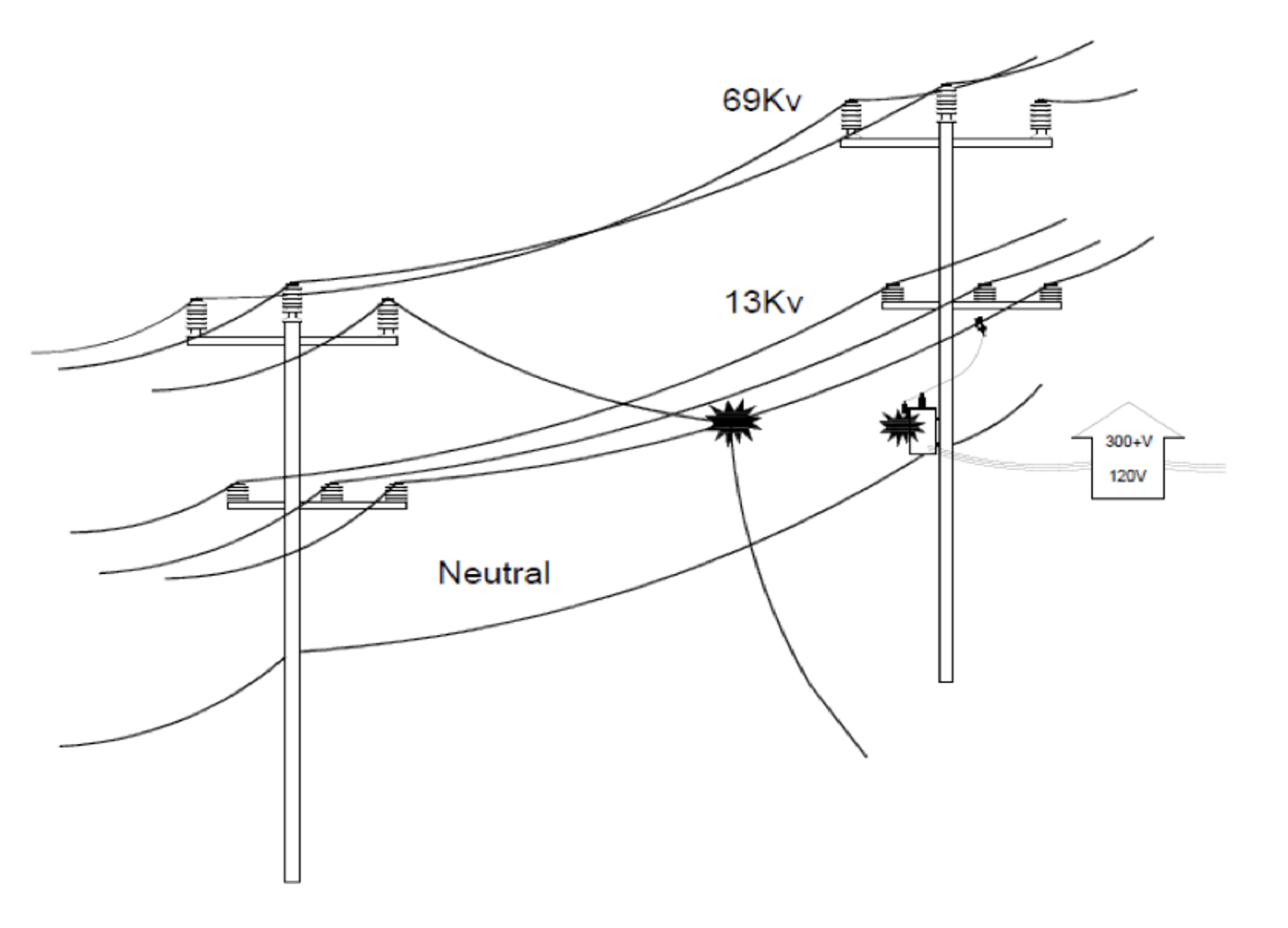
La mitigación propuesta era proveer pararrayos contra sobrevoltajes expiatorios que fallarían de una forma predecible, llamada una configuración de “palanca” para asegurar una falla de línea a tierra de impedancia baja. En la Figura n.° 17 se muestran las implementaciones de este concepto, con el uso de pararrayos de sistemas de distribución tipo “estación” a intervalos periódicos.

Se podrían considerar pararrayos de servicio liviano para proteger los circuitos de distribución que se muestran en la Figura n.° 1, especialmente, si se considera que las corrientes pico más altas que fluyen en los pararrayos son de alrededor de 5 kA. Sin embargo, no existe garantía de que varios pararrayos de servicio ligero en paralelo compartirían por igual la carga excepcionalmente grande de un contacto de una línea de transmisión. Existen algunas opciones que se pueden considerar para combinar ambos esquemas de protección en una sola modernización:

• pararrayos de distribución con dos nominaciones de voltaje y energía diferentes, especialmente con pararrayos de servicio pesado con MCOV más bajo en los postes seleccionados con resistividad de suelo y Z_f baja o

• en base a una cascada de fallas de pararrayos de servicio liviano para proveer el camino de impedancia baja de larga duración deseada a tierra.

Conclusiones

Colocar pararrayos contra sobrevoltajes en las seis fases de los dos circuitos de distribución, que se muestran en la Figura n.° 1, provoca un aumento significativo en los coeficientes de acoplamiento de los circuitos de transmisión no protegidos. Se computa que la corriente crítica se duplicaría, lo que generaría un factor de mejora de cinco en la tasa de apagones en la línea de transmisión, cuando se coopera para permitir una línea de distribución construida por debajo.
Una línea construida con pararrayos en las seis fases de distribución y una impedancia a pie de tierra de 200 Ω tendría el mismo desempeño que una línea con una impedancia a pie de tierra de 20 Ω y sin pararrayos en el circuito de distribución construido bajo la línea.

El acoplamiento modificado por el efecto corona genera una mejora significativa en el desempeño calculado en condiciones de arco inverso. Sin embargo, la mayor parte de esta ganancia se recupera cuando otros factores, como el bias voltaje del sistema instantáneo, el retorno lento de las reflexiones de los efectos corona y la caída de voltaje no cero a través del LSA, se incluyen en el cálculo del arco inverso.

El montaje rígido o semirrígido de pararrayos contra sobrevoltajes en los circuitos de distribución se simplifica, en muchos casos, si se utilizan aisladores tipo poste.

Tener pararrayos en cada aislador de una distribución construida bajo línea también entrega cierto grado de protección contra el contacto de circuito cruzado. Una modernización exitosa puede requerir seleccionar pararrayos tipo “estación”, colocados a intervalos de 1 a 10 km, que absorban la mayor parte de la energía en la exposición al contacto del sistema cruzado y que fallen de la manera deseada con corto circuito (palanca).

Referencias
[1] INMR, “Gallery of Transmission Structures – Wallpaper Oct 16,” Zimmar Holdings Ltd. / INMR, October 2016. [Online]. Available: https://www.inmr.com/gallery/. [Accessed 10 07 2019].
[2] W. A. Chisholm and S. de Almeida de Graaff, “Adapting the Statistics of Soil Properties into Existing and Future Lightning Protection Standards and Guides,” in 2015 International Symposium on Lightning Protection (XIII SIPDA), Balneario Camboriu, Brazil, 28 September – 2 October 2015.
[3] IEEE, IEEE Guide for Improving the Lightning Performance of Transmission Lines, Piscataway, NJ: IEEE Standard 1243-1997, Reaffirmed 2008, September 2008.
[4] EPRI, Transmission Line Reference Book, 345 kV and Above, Second Edition, Palo Alto, CA: EPRI, 1982.
[5] CIGRE WG 33.01, Guide to Procedures for Estimating the Lightning Performance of Transmission Lines, Paris: CIGRE Technical Brochure 63, 1991.
[6] A. R. Hileman, Insulation Coordination for Power Systems, New York: Marcel Dekker Inc., 1999.
[7] EPRI, EPRI AC Transmission Line Reference Book – 200 kV and Above, Third Edition (the Red Book), Palo Alto, CA: EPRI 1011974, December 2005.
[8] EPRI, Transmission Line Reference Book: 115-345 kV Compact Line Design, Palo Alto, CA: EPRI 1016823,
2008.
[9] EPRI, “Guide for Transmission Line Grounding: A Roadmap for Design, Testing and Remediation,” EPRI, Palo Alto, CA, 2004. 1002021.
[10] CIGRE WG C4.407, Lightning Parameters for Engineering Applications, Paris: CIGRE Technical Brochure 549, August 2013.
[11] J. Takami and S. Okabe, “Observational Results of Lightning Current on Transmission Towers,” IEEE
Transactions on Power Delivery, vol. 22, no. 1, pp. 547-556, January 2007.
[12] W. Chisholm and W. Janischewskyj, “Lightning Surge Response of Ground Electrodes,” IEEE Transactions on Power Delivery, vol. 4, no. 2, pp. 1329-1337, April 1989.
[13] CEATI Technologies, “Guidelines for the Installation of Surge Arresters on Sub-Transmission and Transmission Lines using Different Structure Designs at Voltages from 69 kV to 345 kV,” CEATI Report T033700-3312A, Montreal, March 2005.
[14] D. Havard, P. Dulhunty, G. Diana, K. Halsan, H.-J. Krispin, J.-P. Paradis, D. Sunkle, B. Wareing, G. Chapman, W. Chisholm, U. Cosmai, T. Furtado, A. Goel, J. Lundquist, R. L. Markiewicz, M. Mito, C. Rozé and e. al., “Interaction of vibration dampers with surge arresters,” CIGRE Science and Engineering, vol. 6, no. 4, pp. 32-45, October 2016.
[15] D. J. Ward, “Overvoltage Protectors – A Novel Concept for Dealing with Overbuilt Distribution Circuits,” IEEE Transactions on Power Delivery, vol. 25, no. 3, pp. 1971-1977, July 2010.
[16] INMR, “Application of Station Class Arresters on Underbuilt Distribution Lines,” 19 06 2018. [Online]. Available: https://www.inmr.com/application-station-class-arresters-underbuilt-distribution-lines-3. [Accessed 05 07 2019].

[inline_ad_block]