While metal oxide arresters are comparatively modern devices, they have nonetheless undergone rapid development since their inception. For example, such arresters were among the first apparatus in power systems to be equipped with polymeric insulation. Progress has also been achieved in improving MO resistor performance, making arresters among the most reliable of all system components.
This edited past contribution to INMR by Prof. Volker Hinrichsen, retired from the Technische Universität Darmstadt in Germany, addressed remaining challenges in development of gapless MO arrester technology, including improved energy handling capability as well as on external grading systems to mitigate uneven distribution of electric field.
Gapless metal oxide arresters are the byproduct of the ‘accidental’ invention of ZnO resistors in 1968 by Matsushita Electric Industrial in Japan. Subsequent development toward overvoltage protection devices for electrical power systems resulted in the first such application by 1975.

Starting in the mid-1980s in the case of distribution class arresters and by the early 1990s for high-voltage station class arresters, MO arresters became one the first types of electrical apparatus to be equipped with polymeric insulation. This soon became state-of-the-art for distribution and is now also increasingly applied on transmission systems.
Moreover, unlike the gapped silicon carbide arresters it replaced, MO technology has also allowed applications beyond traditional overvoltage protection at substations. These new applications have included multi-column UHV station arresters for systems above 1000 kV, HVDC arresters in converter stations (valve protection arresters being the most important), distribution and transmission line arresters (with or without a series gap) and arrester banks in flexible AC transmission systems for overvoltage protection of series capacitors in case of line faults. The most recent development sees MO arresters applied as indispensable energy absorbers in emerging HVDC circuit breakers.
Energy handling capability and potential electrical degradation of MO resistors has been one of the concerns since the start. Due to permanent connection to the line, a gapless MO arrester can theoretically suffer thermal runaway after excessive energy input or due to deterioration of its non-linear voltage-current characteristic. Fortunately, electrical degradation is no longer regarded as a risk for experienced arrester manufacturers. Moreover, demanding test requirements in current standards now hopefully avoid any setback from the high level already achieved.
However, today’s less conventional applications require different approaches when specifying and verifying energy handling capability than only looking at line discharge, as was previously the case for station class arresters. Supported by work at Cigré, test standards have now been improved to cover all aspects of modern-day arrester applications, though more still has to be done. At the same time, IEC and IEEE arrester test standards have been harmonized, resulting in a dual logo standard on all types of line arresters as prepared by a joint IEC and IEEE WG (Project IEC/IEEE 60099-11).
One of the most interesting developments these days is that simulation tools have become very powerful. This has made it possible to optimize EHV and UHV arrester designs with respect to external grading system and thermal stability limit using non-linear, fully coupled electro-thermal simulations. This, in turn, has opened the door to designing UHV arresters with reduced need for full-scale laboratory testing, which is difficult at these voltage levels. The trend to avoid full scale testing is also supported by ‘smart’ approaches in the standards in regard to dielectric withstand tests. For example, based on sufficient experimental experience, the need for such tests can be avoided if certain minimum clearance requirements are fulfilled. Thus, UHV arresters can be developed and qualified without need for full-size 1000 kV test facilities.
Energy Handling Capability
Surge arresters act to limit overvoltages caused by transient lightning or switching phenomena. At the same time, they must avoid tripping of a line. In that latter role they do not need to limit the voltage to zero but rather to a level that can be safely withstood by apparatus in the system. This means that arresters must be able to dissipate power during passage of a current to ground and, consequently, absorb energy. Some energy handling capability must therefore be specified for an arrester. Historically, this was done in different ways for station and for distribution class arresters.
The most challenging duty for station class arresters was considered a line discharge. A transmission line that is suddenly disconnected from the system and (depending on actual load situation and time instant of de-energization), charged to an overvoltage of several p.u. of system voltage (1 p.u. = Us∙√2/√3), discharges through the connected arrester. The arrester therefore has to absorb the energy stored in the capacitances of the line(s). The energy thus absorbed depends on initial overvoltage, line length and arrester switching current protection level, which determines to which degree the line is discharged.
It makes sense in the exclusive case of this particular scenario to specify line discharge capability rather than an energy, which in the case of gapped SiC arresters had been shared among the arcs in the series gaps as well as the resistors. In fact, up until 2014 IEC arrester standards defined energy handling capability of station class arresters this way, i.e. by line discharge classes LD 1 through LD 5. A line discharge class, however, does not help the system planner with applications such as capacitor bank protection nor, in general, when there is no discharge of a line. It is also not applicable to emerging UHV systems, which require energy handling (basically due to the arresters’ low protection levels and thus their involvement in temporary overvoltages) that is far beyond any so far specified line discharge class.
By contrast, the main purpose of distribution class arresters is to divert charge, as for example brought to a line by a direct lightning strike to ground. It then becomes reasonable to specify a charge transfer capability rather than an energy handling capability. Of course, energy is also being dissipated during charge transfer. But arresters with lower protection level have to absorb less energy at a given amount of charge than an arrester of higher (and thus worse) protection level. Therefore, charge transfer capability better specifies the arrester characteristics required.
Independent of such considerations, energy handling capability of distribution arresters was related to the ability to carry a 4/10 µs high-current impulse current of up to 100 kA for two times in the type test – something that has little to do with any stress realistically encountered in a power system. Since the specified time and amplitude tolerances of the high-current impulse are very large, the charge and energy impact on an arrester in this scenario is not really well defined.
Finally, a clear distinction must be made between:
1. thermal energy handling capability, which aims to avoid thermal runaway of an arrester;
2. single impulse energy handling capability, which can be survived by the arrester for one individual overvoltage event without mechanical damage to its MO resistors; and
3. repeated single impulse energy handling capability, a similar aspect as in point 2 but for many times during the arrester’s service life. Manufacturers have tried to cover this aspect by a ‘long duration current impulse capability’. But since no related test procedure was specified in any standard, it became the manufacturer’s decision on how to specify test conditions, which came to be done in different ways.
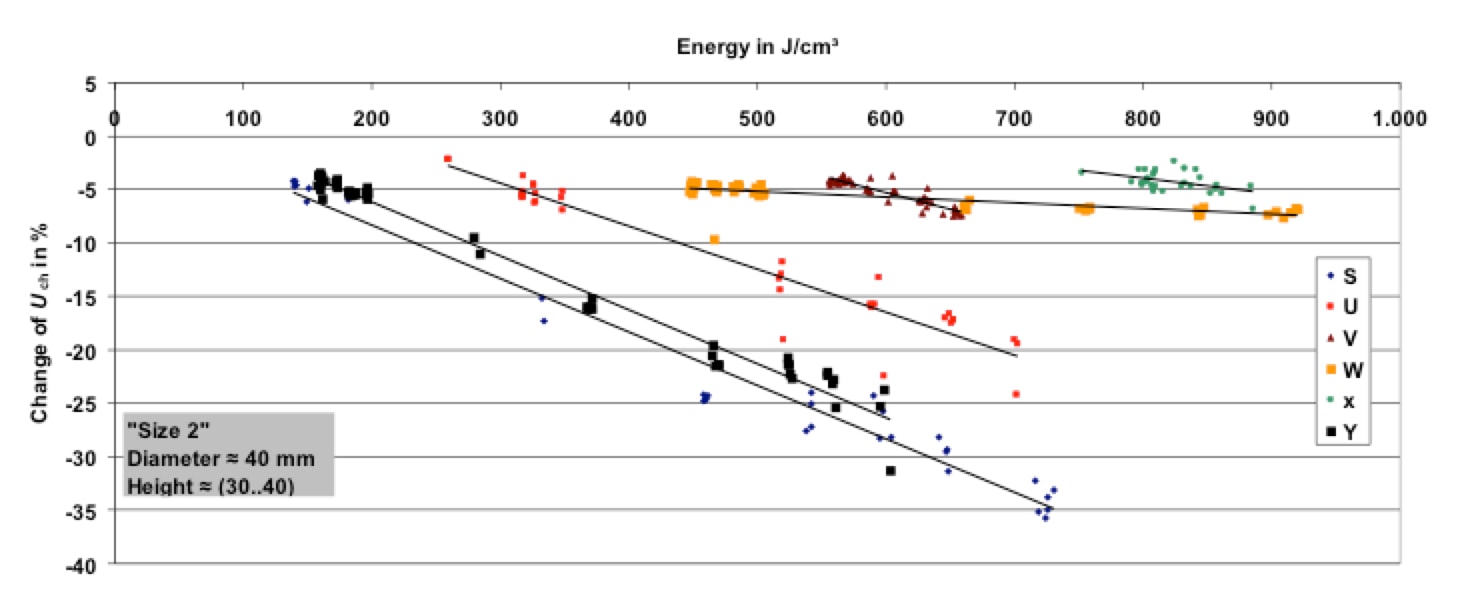
The above was the justification and motivation for changing test philosophies in IEC arrester standards, which, after long discussion, resulted in the present standards. The basis was laid by Cigré Working Group A3.17 and later by WG A3.25, which prepared two Technical Brochures that addressed energy handling issues. Fig. 2 shows the basic finding when it comes to single energy handling capability, in this case for MO resistors typical for use in station class arresters.
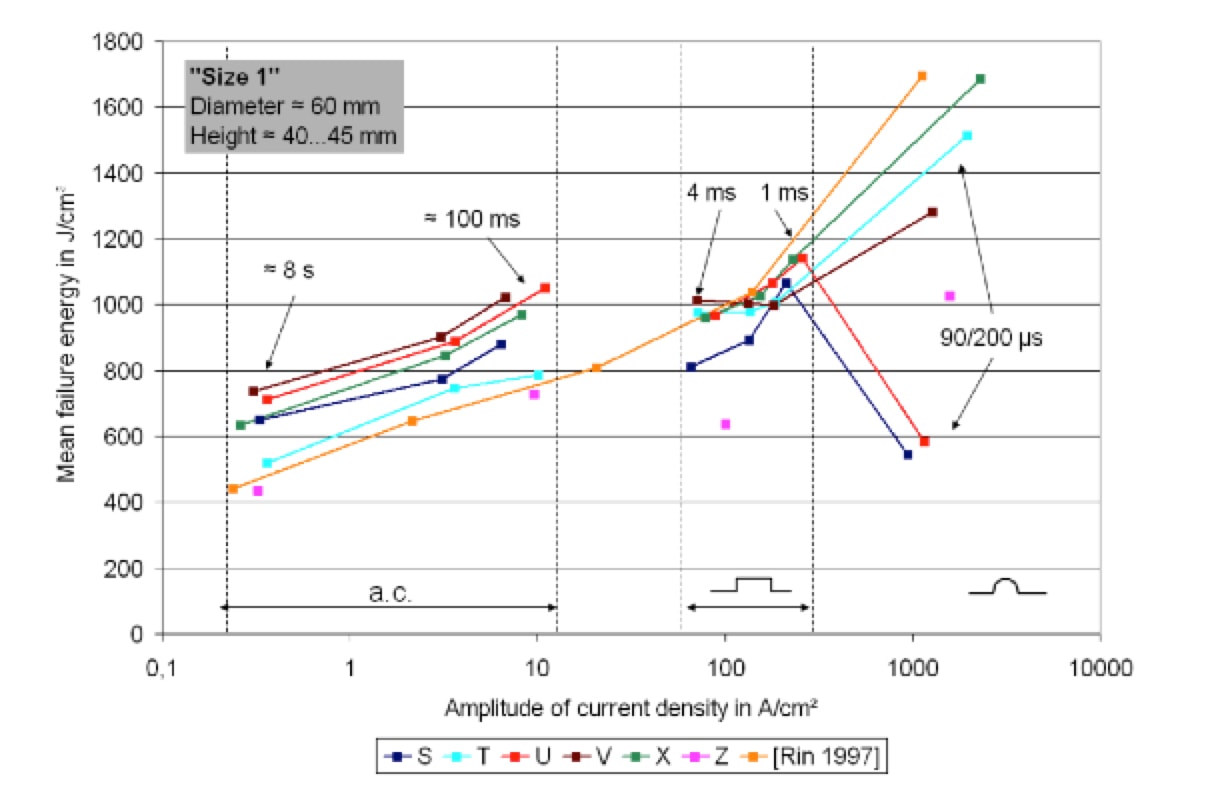
Important lessons from this investigation involving thousands of MO resistor samples supplied by different manufacturers worldwide were:
• Mean single-impulse failure energies vary approximately from 400 J/cm³ to 1200 J/cm³ for very fast impulses and even up to 1700 J/cm³. This is far above the typical design energy of 200 J/cm³.
• Energy handling capability increases with current density amplitude basically the same way as had been reported earlier. However, mean failure energy increases by up to 70% (on average by at least 20%) compared to some past investigations. This is an impressive demonstration of the development of MO resistors in terms of better material homogeneity. Still, the wide spread among the different makes, by a factor of 1.7, should motivate manufacturers to continue work toward optimizing their products.
• A key observation was that some MO resistors typically exhibit the expected increase in energy handling capability for extreme values of current density. But there also exist some makes that showed a decrease in failure energy down to values of only 500 J/cm³. The reason is a different dominant failure mechanism, i.e. dielectric failure of the coating, resulting in flashover. Until now, the ‘repetitive charge transfer rating’ test with 90/200 µs impulses has been the most challenging energy-handling test for MO resistors used in line arrester applications. While these results seem promising and lead to the question why design energy is specified so low, subsequent endurance tests have put them into perspective:
For repeated energy injection, injectable energy differs for different current densities. The higher the current density of the impulses, the lower the energy that can be injected without pre-damaging the MO resistor. The energy level that can be handled without pre-damaging the MO resistors by repeated energy injections in the case of AC stresses is close to the level of single-impulse energy handling capability and thus comparatively high. By contrast, for long duration current impulses, e.g. 2 ms virtual time duration, it is close to the typical design energy for standard arrester applications, namely in the range of 200 J/cm³.
These investigations have shown that the single-impulse energy handling capability of MO arresters is surprisingly high – many times higher than typically specified rated energy handling capability. However, if single-impulse stress at such high levels occurs repeatedly, much lower values would be acceptable so as not to damage the arrester. Overall, an arrester has a fairly good chance to ‘survive’ a few energy inputs much higher than its rated energy as long as the thermal stability limit is not affected. This might be the reason arresters have had such an excellent service record, given that excessive energy input is a rare event under standard system conditions. However, if this occurs more often, permissible injected energy definitely must be limited to the rated energy.
In the case of often-repeated, high-energy long duration current impulses, the leakage current region of the voltage-current characteristic is affected only negligibly. This means that this kind of stress has no negative effect on the arrester’s thermal stability limit. Station class arresters in substations benefit from this since very steep and short high-energy impulses are rare at these locations. But high-current impulses will affect the leakage current characteristic to differing degrees, depending on make of the MO resistor (see Fig. 3).
This is therefore an issue for distribution or for gapless line arresters. However, since such stress is generally imposed in all thermal stability tests during type testing, the arresters have proven thermal stability even under the impact of a deteriorated leakage current characteristic. That means this effect is sufficiently covered by type tests and thus not an additional risk during service.
Energy Absorbers for HVDC Circuit Breakers
HVDC technology for far distance transmission of electric power has been applied for more than 60 years and is rapidly emerging towards higher voltage levels ( 800 kV in service; 1000 kV under development). Since voltage sourced converters (VSC) in modular multilevel technology (MMC) are becoming state-of-the-art, meshed HVDC overlay grids are also becoming a realistic option. A meshed grid requires circuit breakers and many proposals have been made for their implementation. Since direct current has no natural zero crossings and as mechanical breakers do need a current zero for current interruption, the zero crossing must be enforced by external circuitry. But this does not solve the problem that, due to the flowing current, magnetic energy is stored in system inductances, which must be absorbed if extreme overvoltages are to be avoided. Every DC circuit breaker, independent of its general operating concept, therefore needs an energy absorber in parallel. This is – naturally – a MO arrester, typically arranged as an arrester bank with many MO resistor columns in parallel. Fig. 4 depicts a basic sketch of the working principle, i.e. a vacuum interrupter with a pre-charged RLC circuit connected in parallel to trigger (by the spark gap SG) and superimpose a high-frequency oscillation to the system current through the interrupter, by which artificial current zeroes are enforced.
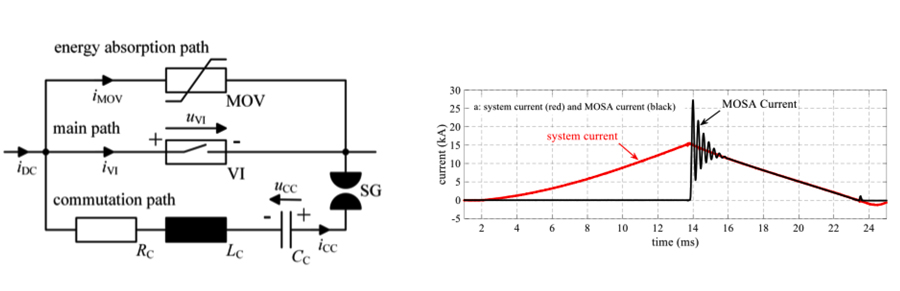
As can be seen, the current through the arrester during the DC current interruption has a characteristic shape: a steep increase to several kilo-amperes and a long lasting decay for some 10 milliseconds. Further on, the arrester might be stressed by a continuous direct voltage as long as the breaker is not disconnected by a series disconnector (not shown in Fig. 4). This is a relatively new stress scenario for MO arresters and which requires investigation of energy handling capability and electrical degradation. Unfortunately, little on this has been published so far. More than 10,000 impulses should be withstood by the arrester, for which reason the typical approach must be an endurance test with current impulse shapes as close as possible to the real application, with underlaid direct voltage stress as a worst case condition and with more than 10,000 energy injections.
All these investigations reported degradation effects in terms of reduced permissible energy per impulse for repeated impulse application, increase of the DC leakage current and increase of the clamping voltage in different degrees depending on make. For example, different commercially available makes from different manufacturers (diameter » 50 mm, height (2.5…7 mm) were investigated and showed much different ageing behavior. A notable example is shown in Fig. 5.
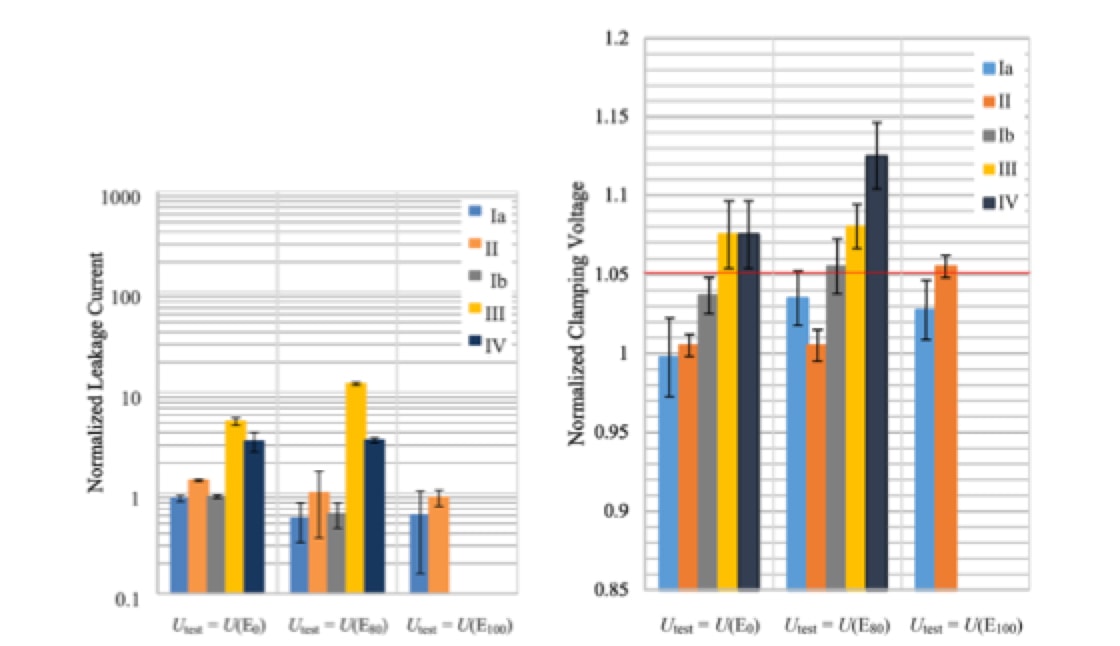
Left: Leakage current. Right: Clamping voltage.
As can be seen in Fig. 5 left, although some makes are nearly unaffected, an increase in leakage current by up to a factor of approximately 10 may occur, depending on make. This is notable but not really an issue so long as the arrester is not permanently connected to the system voltage. But clamping voltage might also be increased by more than 12% (see Fig. 5 right), which cannot be neglected and might disqualify that particular make for the intended application.
Arrester standards in general allow a 5% maximum increase of the residual voltage after any energy stress. It is further concluded from these investigations that due to the exclusively unipolar stress, DC stable material (e.g. qualified by the accelerated ageing test procedure of IEC 60099-9:2014, Clause 9.11) should be used – even if no permanent direct voltage is applied. Finally, there are clearly some makes on the market that can be used in HVDC breaker applications without restriction.
In another investigation, only one particular make was tested (diameter » 70 mm, height » 6.35 mm). Eleven samples were stressed by up to 15,000 energy injections. At the end, a failure energy test (i.e. injection of a high AC current to breakdown) was performed and compared to the known mean failure energy of new samples. Fig. 6 shows one noteworthy result on electrical degradation.
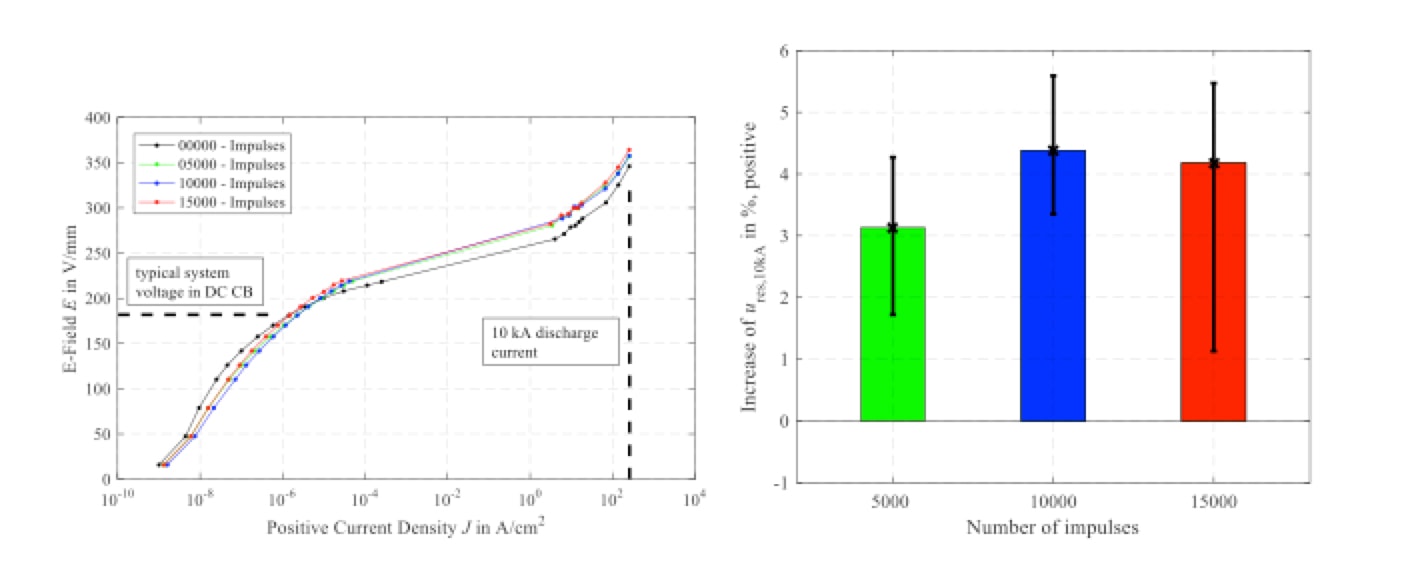
This investigation also revealed that leakage current as well as clamping voltage will be increased by this stress scenario, expressed by counter-clockwise rotation of the U-I-characteristic in Fig. 6 left. In this example, the 5% criterion of allowed maximum increase in residual voltage was met by most samples with only a few minor exceptions (see Fig. 6 right). In the final failure energy tests, the failure energy of pre-stressed samples turned out to be unchanged or even increased.
One of the lessons from this work is that application of today’s commercially available MO arresters as energy absorbers in HVDC breaker applications is certainly possible. The material should be DC stable even if the system voltage is not permanently applied. Samples that are not DC stable would typically fail during the endurance test. It has to be kept in mind that leakage current as well as clamping voltage will increase over the arrester’s full lifetime but obviously stay within acceptable limits depending on make. It should, however, be discussed in the future whether the 5% criterion in arrester standards, which presumes only moderate stress (e.g. 20 injections of rated energy) can be applied in this case, where more than 10,000 energy stresses are considered. Under these conditions, perhaps a greater change could or must be tolerated. Nevertheless, these investigations indicate that the concept of energy absorbers made up of MO resistors will work. Further research will have to be performed to better generalize these findings, which were based on only a limited number of makes and samples.
Arrester Banks
Among the benefits of gapless MO arrester technology is that many MO resistor columns can be connected in parallel and, if current sharing is carefully considered, they can evenly share energy stress. Current sharing is not an issue in the region of nominal discharge current (e.g. 10 kA), where the exponent of non-linearity is typically a < 5. A 1% lower residual voltage of any MO resistor column in a parallel-connected arrangement then means a 5% increase of current in this column. This is common practice for EHV (800 kV) and UHV (> 800 kV) systems, where several columns are typically connected in parallel. However, in the switching current region of the U-I characteristic, for instance 100…500 A, the exponent of non-linearity is higher, i.e. on the order of a = 25. Current increase due to a 1% lower residual voltage will then be 28%. This makes it challenging to manufacture huge arrester banks with sometimes 100 resistor columns in parallel and this solution may not work well in all cases.
One typical application is overvoltage protection of series capacitors where, in the event of a line fault, the full short-circuit current would flow through the capacitor. This would linearly increase the voltage drop across the capacitor unless the current was commutated to an arrester connected in parallel. Energy absorbers for emerging HVDC circuit breakers may also be of this scale.
Eventually, an individual resistor column in a bank may be overloaded and has to be taken out of service. In such cases, it is recommended to install ‘hot’ spare columns. These are exposed to exactly the same electrical stress as all neighboring columns. If these become spent, it is recommended not to mix old and new columns, which means replacement of the entire arrester bank.
Given that this is unsatisfactory from an economic point of view, investigations have been performed to determine if old (i.e. aged) and factory-new MO resistor columns can be mixed. Since in such an investigation one is looking at changes in residual voltage of << 1%, measurement of voltage given its typical uncertainty of 3% becomes meaningless. Thus, all measurements in this work were evaluated by their changes in the switching impulse current range relative to a reference column connected in parallel. The test specimens were columns of 12 MO 100 mm diameter resistors in series. Fig. 7 indicates the main result.
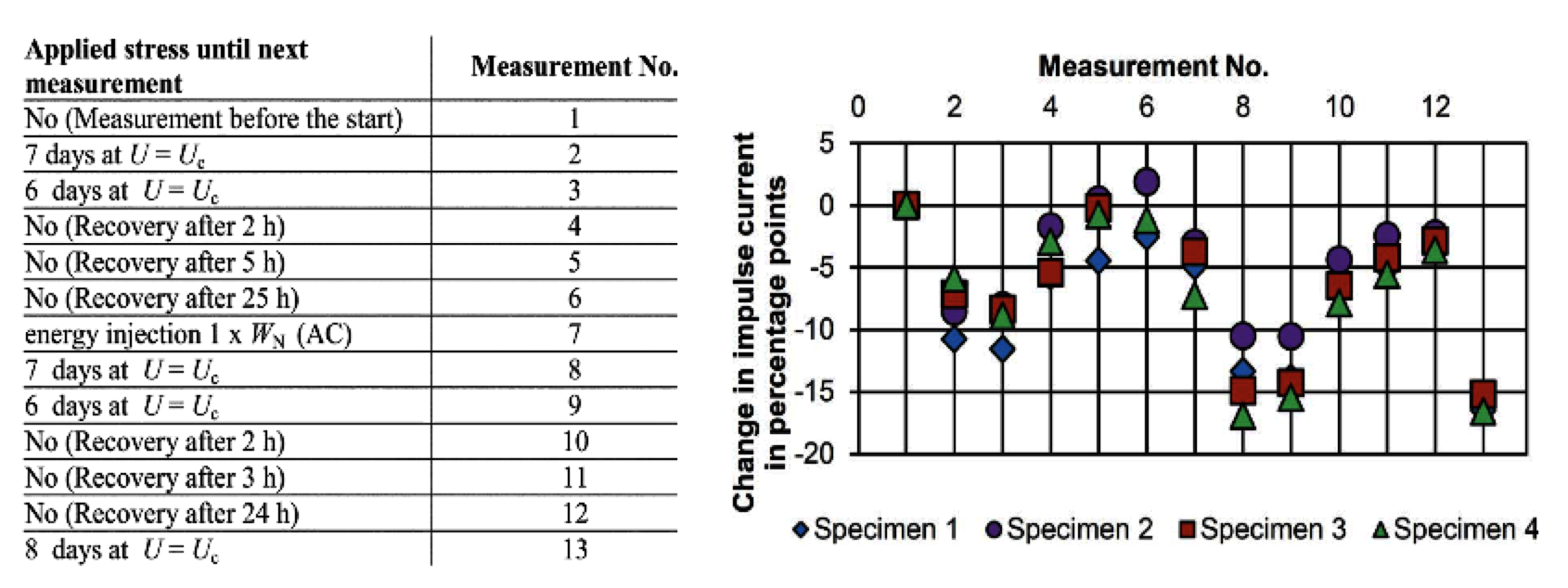
The left part of Fig. 7 shows the test cycle, which consists of 13 days with applied power-frequency voltage U = Uc, one day with no voltage applied, injection of full rated energy by high alternating current injection, 13 days with U = Uc applied, one day without voltage applied and finally 8 days with U = Uc applied. The outcome is shown at the right of Fig. 7. In summary, application of power-frequency voltage results in a (10…15) % decrease in switching impulse current compared to the reference column (corresponding to a 0.5% increase in residual voltage under the assumption a = 25). But one to two days without any voltage applied results in a near total recovery to the initial stage.
The conclusion is that individual columns, which are usually matched in the factory to the reference column, can be added to an arrester bank just two days after de-energization with no adverse impact on current sharing. This finding suggests that replacement of complete arrester banks is not necessary. Instead, individual columns can be installed any time so long as the same make of MO resistors is still available and the original reference column has been stored in the factory. Of course, this result is limited to the particular make of MO resistors investigated, although different production batches were used. Ideally, it should be verified and for other makes of MO resistors as well. Moreover, given that this research is also interesting for energy absorbers in HVDC circuit breakers, similar investigations should be performed under typical DC stress conditions.
Simulating Design of External Field Grading
Due to the impact of stray capacitances to earth, there is uneven potential distribution along AC arresters more than 2 m high, meaning that top units are exposed to higher voltage stress than are the bottom units. This results in higher power losses and therefore higher temperatures. Voltage stress across the top units is partly reduced by the self-grading effect that becomes effective when MO resistors are operated closer to the breakdown region of their U-I-characteristic (termed above reference voltage in arrester standards), thereby becoming more conductive. But the cost is heat generation due to increased power losses.
To limit such temperature increase to acceptable values, external grading rings (and in a few cases internal grading capacitors as well) are typically applied to compensate for the effects of stray capacitances to earth. Increased operating voltage stress of upper MO resistors is already considered in arrester test standards, e.g. in the specification of the “Test to verify long term stability under continuous operating voltage” (colloquially: “accelerated aging test”) in Clause 8.4 of (IEC 60099-4:2014, 2014). Moreover, Annex F of IEC 60099-4:2014 provides a “Guide for the determination of the voltage distribution along metal-oxide surge arresters”. However, for a variety of reasons, this only partly covers such problems.
First of all, only voltage increase is currently considered. But since arrester operation is ultimately also affected by increased temperatures, their equalization or reduction must be the goal of any optimization efforts. Secondly, the Guide for determination of voltage distribution addresses non-linear electrical effects but not resulting thermal effects. It also provides sparse information on how to model a real, non-axisymmetric 3D arrester configuration by an equivalent 2D arrangement that can be simulated at lower expense. Moreover, while application of virtual grading rings is recommended, detailed information on their dimensioning and positioning is not given. Finally, the impact of uneven temperature distribution along the arrester axis on its thermal stability limit is, in principle, unknown.
The arrester community has long had to deal with these issues yet still gained experience in dimensioning external grading systems of EHV arresters up to 800 kV system voltage level. But now, UHV arresters are emerging where dimensions of external grading rings have to be reduced compared to the optimum case so as to be able to dielectrically withstand the arrester’s own switching impulse protection level. A range of questions has therefore come up: to what degree can temperature imbalance caused by suboptimal grading be accepted? What are the highest acceptable temperatures on top arrester units? How is thermal stability limit affected by increased temperature?
Unfortunately, these questions have never and still cannot be answered by full size laboratory tests since injection of rated impulse energy into full-scale EHV and UHV arresters is not possible. As such, tests on thermal stability are currently performed on small thermally equivalent prorated sections and assumed to yield conservative results, i.e. that err on the side of safety. But even experimental verification of this assumption is not possible.
Now, the time has come to make increased use of simulation approaches. Today’s commercially available FEM simulation software tools offer a solution to non-linear, fully electro-thermal coupled problems. But work remains to be done. For example, 3D structures have to be converted into 2D to reasonably reduce calculation efforts. Also, complex heat transfer mechanisms, i.e. radiation, convection and conduction, must be simplified to equivalent heat transfer numbers. Correct experimental determination and theoretical modeling of the non-linear electric characteristics of MO resistors (electric field and temperature dependent conductivity and permittivity) is challenging. Even minor details of the laboratory environment cannot be overlooked in the simulation if good agreement between simulation and experimental results is to be achieved.
Two recently published collaborative Ph.D. theses, indicated in the References section at the end, have dealt with this complex matter and below is a brief summary of findings:
1. Impact of Grading System on Thermal Stability & Thermal Energy Rating
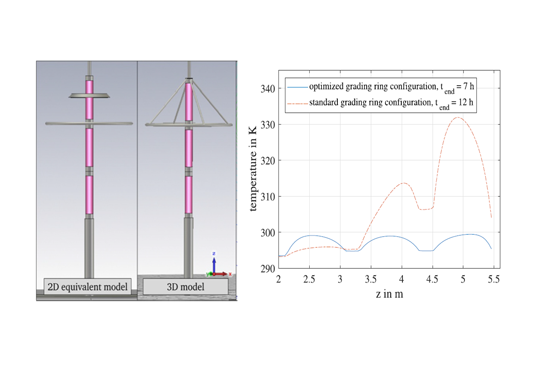
The thermal stability limit of an EHV or a UHV arrester can be experimentally estimated by slow energy injection at applied power-frequency voltage some 30% above the arrester’s continuous operating voltage. This takes time – up to 30 minutes – and does not yield the exact stability limit because the heat capacitances of all passive arrester components (flanges, internal metallic spacers, housing, etc.) are also thermally ‘charged’ during this time. But once a model has been established that gives simulation results that agree with experimental results in the case of AC heating, the real thermal stability limits under the impact of impulse energy injection, can be determined using only simulation, as would be the case under real service conditions. Fig. 1 shows such a comparison for a typical 550 kV arrester (h = 4.2 m, Uc = 300 kV, Ur = 375 kV, U10kA = 960 kV).
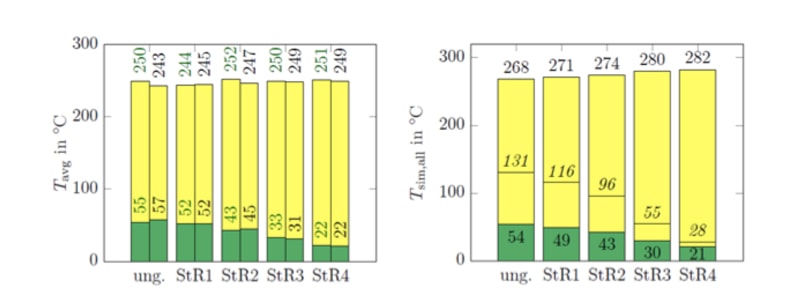
From Fig. 8, it can be concluded that:
• measurement and simulation for the AC heating case are in excellent agreement (left: comparison of the two bars for each configuration). This demonstrates the power of modern simulation approaches;
• spread in axial temperature distribution is wide in the ungraded case (ung.: average = 54°C, max. = 131°C) and extremely narrow in the optimally graded case (“StR4”: average = 21°C, max. = 28°C);
• thermal stability limits in terms of mean temperatures, averaged over the full arrester height, are virtually unaffected by the grading configuration. This means that an ungraded arrester has the same thermal stability limit in terms of average temperature as an optimally graded one, independent of the excessively high temperatures in the top units, as was also published in (Hinrichsen, Giessel, & Tuczek, Thermal Stability of HV and UHV Arresters with Reduced Grading Systems, 2015);
• thermal stability limits in case of impulse energy injection are (25…33)°C higher than after AC energy injection (compare left and right of Fig. 1). This demonstrates the drawback of purely experimental approaches, which are overly conservative though at least on the side of safety.
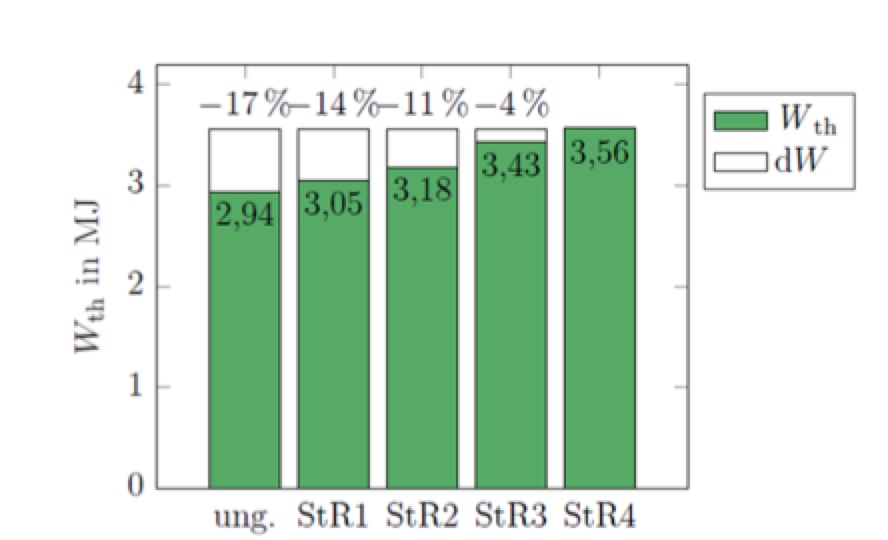
Due to resulting higher average steady state temperatures, an arrester can handle less energy if less effective grading measures are being implemented. However, the difference in thermal energy handling capability between an absolutely ungraded and an optimally graded arrester is only 17%, as shown by simulations (see Fig. 2).
One of the lessons from these investigations using modern simulation approaches is that aiming at optimal potential grading of EHV and UHV arresters is not as important as has been assumed. Any axial temperature imbalance along the arrester axis has little impact on thermal stability limit. Rather, only average temperature along the arrester axis is important. While reduction in thermal energy rating due to non-uniform temperature distribution must certainly be regarded, there is no real risk that under-graded UHV arresters will be less reliable or suffer thermal runaway due to temperatures at their top being so high. Furthermore, use of internal grading capacitors has to be questioned since these constitute additional active elements that might suffer electrical ageing. They may help increase thermal energy handling capability but are not necessary for thermal stability. Finally, these investigations also suggest that experimental approaches in arrester standards to verify thermal stability yield results on the ‘safe’ side.
This is reassuring but may result in safety margins that are unnecessarily large. For instance, actual limits of thermal stability are typically under estimated by type test procedures. At the same time, it is difficult to challenge such established approaches that have presumably contributed to the excellent service history of arresters.
2.Optimizing External Grading & Prediction of Thermal Stability Limit
Two additional examples of the benefits of present simulation approaches are shown below: the first is with respect to automated optimization procedures, as demonstrated for grading ring optimization; the other is effective prediction of thermal stability limits, once the electro-thermal model of an arrester has been established.
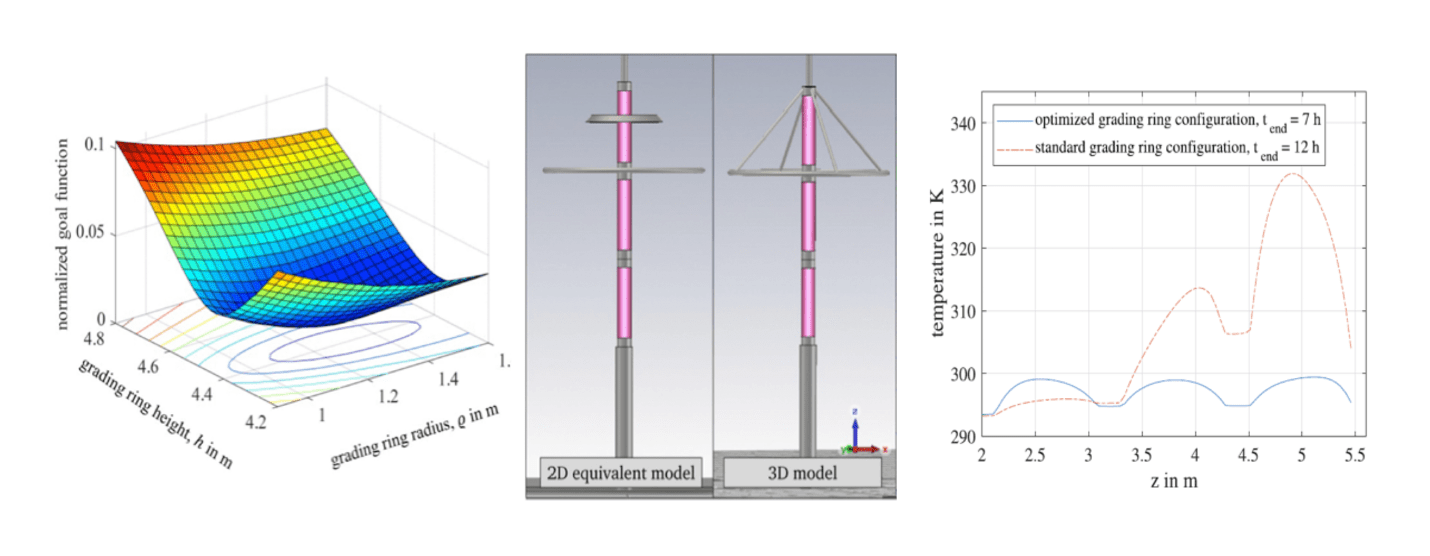
Middle: Resulting grading ring configuration in 2D model and in real 3D arrangement.
Right: Achieved uniform steady state temperature distribution (blue) compared to initial ring configuration (red).
It has been shown that the virtual grading electrode proposed in IEC 60099-4:2014 for 2D simulations of arresters can be improved by assuming a cone shaped screen rather than the proposed ring electrode, and that its dimensions and position can automatically be optimized by especially developed algorithms in order to perfectly model the real 3D arrester configuration. Further, an automatized procedure has been developed to optimize an arrester’s grading ring with respect to the axial distribution of the electric field, power loss and temperature becoming as uniform as possible. For the chosen example of a 550 kV arrester, a global optimum (the minimum of the normalized goal function in Fig. 10) could be found, in this case for an installation height of the ring of 4.4 m from ground and a ring diameter of 1.2 m, see Fig. 10, left. As can be further seen from Fig. 10, middle, such a ring might be unrealistically large, and as explained above, especially this optimization might not be the most important one, but the example demonstrates the high potential of automatized arrester optimization by simulation approaches in general. The result is rather impressive because the outcome is an extremely uniform steady state temperature distribution along the arrester axis, see Fig. 10 right.
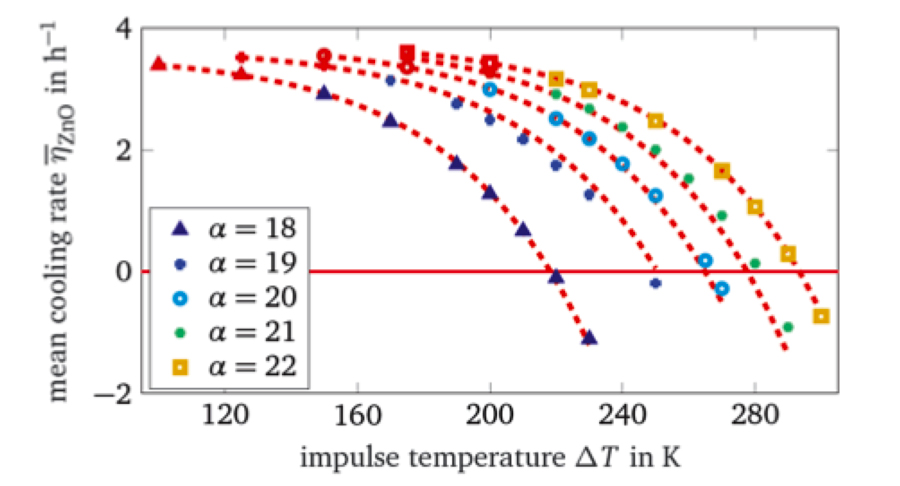
As discussed above the thermal stability limit of an arrester is not easy to assess even if simulation approaches are applied, because each variation of a design parameter requires several simulation runs in order to determine the maximum amount of energy injection, for which a thermal runaway will not occur. In (Späck-Leigsnering, Electrothermal Modeling, Simulation and Optimization of Surge Arresters) a procedure is presented that allows, just by two short simulation runs, a prediction of the thermal stability limit of an arrester configuration, for which the general electro-thermal model has been established and that shall subsequently be optimized by varying e.g. the grading system or the U-I-characteristic of the used MO resistors. For this purpose a cooling rate, averaged over the arrester height, is introduced. As long as it has positive values (> 0) after an energy injection, thermal stability is achieved. The thermal stability limit is found for the amount of energy injection (or temperature increase, respectively) that results in a cooling rate of ≤ 0..
Fig. 4 shows an example, in which the non-linearity exponent, α, of the switching impulse current region of the U-I-characteristic has been varied in a range from 18 to 22. As it can be seen the α-value has a strong impact on the thermal stability limit, which is found to be in a range of the temperature step (due to energy injection) from 220 K to 300 K. It is important to note that each of the dashed curves is extrapolated based on only two simulations, which are indicated by the red markers at the beginning of the curves. The markers colored other than red stand for full simulations each that were performed just in order to compare the prediction with an actual full simulation result. Excellent agreement between the extrapolated curves and the actually calculated points is achieved. This demonstrates the effectiveness of the approach. Only two simulations have to be performed for each parameter variation.
The basic message of this chapter is that future further arrester developments can, should and will be more and more based on simulation approaches. Modern simulation tools allow simulation of nonlinear, fully coupled electro-thermal problems. As, on the other hand, erection and operation of high-voltage test halls becomes increasingly difficult when aiming at the UHV voltage levels of actually up to 1200 kV and maybe even higher values in the future this option should be increasingly applied and particularly be further developed. Still some special algorithms beyond the commercially available standard software tools need to be designed, but this is definitely a profitable investment.
Development of Arrester Standards
Progress in further developing international arrester standards has been good. For example, in 2014, the concept of energy handling specification and testing was introduced into IEC standards. Subsequently all other IEC arrester standards were re-worked to be in line with these new approaches, including IEC 60099-8:2017, 60099-5:2018, 60099-6:2019. The most recent standard was published in 2019. Another requirement in regard to new standards, namely providing requirements and test procedures for UHV arresters, has been covered by IEC 60099-4:2014. IEC standardization is therefore able to support manufacturers and users both in existing and in novel arrester applications. The stability date of IEC 60099-4:2014 is 2020. For the next edition, apart from fixing editorial bugs, improvement in complex items such as short-circuit testing in general or test requirements on separable and dead-front arresters are being discussed in IEC TC37 MT4, based on the feedback from manufacturers, users and test laboratories.
The situation is similar for IEEE arrester standards. Final publication of the next revision of IEEE C62.11-2012, the main standard took place late last year. Also, great effort has been made toward harmonizing IEC and IEEE arrester standards. The respective working groups have had joint meetings at least once a year and it is expected that the most important test requirements will be unified within the coming several years.
An even more consistent approach has been chosen for future standardization of line arresters, which are gaining importance worldwide. Today, these arresters are internationally covered by IEC 60099-4:2014 and 60099-8:2017 as well as IEEE C62.11-2012. The plan is to develop a new IEC/IEEE dual logo standard applicable to all types of line arresters without any exception (distribution, station, gapless or externally gapped, AC and DC applications) (IEC TC37, PT60099-11). This is a challenging task, for instance as there is virtually no experience with DC applications, and the approaches of the Japanese standards are partly different from those of the IEC or IEEE standards. However, line arresters were “invented” in Japan, and Japan has the largest operating experience with line arresters. This must certainly be recognized and reflected in this future standard.
Another quite challenging project of the responsible IEC working group is the development of “Test rationales”, an approach adopted from the respective IEEE working group (IEEE SPDC WG 3.3.11). The idea is to recall and publish motivation and justification of existing test requirements and specifications (which has turned out to be very difficult in many cases, even for experienced arrester specialists) and to write test rationales for all new test requirements and procedures in the future. Actually it is intended to publish the “Test rationales” as an IEC Technical Report (TR) within the 60099 series of standards.
Summary & Conclusions
Gapless MO arresters are relatively young devices in electrical power systems, brought to the market in 1975 and being standardized from around 1990. Until now they have undergone an impressing development, and currently they are among the most reliable equipment in power systems. Exceptions do exist, but they are typically related to special and occasionally underestimated system conditions, insufficient dimensioning, often due to a lack of expertise, or just quality problems, with mechanical sealing deficiencies being at the forefront. New arrester applications have become possible only by this novel arrester technology, such as UHV arresters, HVDC arresters, line arresters with and without series gap, huge arrester banks in FACTS and, as a most recent development, as energy absorbers in HVDC circuit breakers. But these applications require approaches in specifying and verifying energy handling capability other than just by line discharges as it was the case in the beginning of arrester standardization. Supported by Cigré work, the test standards have permanently been improved in order to cover all aspects of today’s arrester applications, though still work has to be done on this way. Very likely more than for any other apparatus the test standards of IEC and IEEE are being harmonized. As one of the most exciting actual developments in engineering, simulation tools have become so powerful that it is currently possible to optimize EHV and UHV arrester designs with respect to their external grading systems and their thermal stability limits by nonlinear fully coupled electro-thermal simulations.
This contribution has focused on energy handling and electric aging aspects, where a couple of lessons had to be learned, and related actual findings have found their way into the arrester standards. It has also addressed the today’s possibilities of simulating arrester operating behavior with the help of nonlinear, fully coupled electro-thermal simulation tools. This has opened the door for designing UHV arresters with considerably reduced need for full size testing in the laboratory. It is anticipated and recommended to make increasing use of these approaches. For instance, many operating aspects of UHV arresters are extremely difficult to assess experimentally, simply for the reason that the necessary large high-voltage test halls are not available in sufficient quantities.
A further emerging MO arrester application will be their use as the indispensable energy absorbers in HVDC circuit-breakers. It has been shown in this contribution that this application is basically possible. But further investigations on different MO resistor makes are necessary to give general statements and recommendations on it and to finally introduce them into the arrester standards. Energy absorbers are typically arrester banks, often made up from a huge number of MO columns in parallel. Such configurations can also be found in EHV or UHV AC long-distance transmission systems, for which FACTS are becoming increasingly important. Arrester banks will also be required for protection of HVDC long-distance transmission cable systems, which are actually in discussion e.g. in Germany. Proper dimensioning of huge arrester banks will, therefore, become a standard design task rather than an exception as it might be the case today. As in such arrester banks thousands of MO resistors are energetically stressed at the same time the risk of failure of individual MO resistors, and consequently columns, is increased compared to standard substation arresters. This requires on one hand an ever better MO resistor quality in terms of material homogeneity and reproducibility, energy handling capability and electrical degradation, and on the other hand economically reasonable strategies for replacement of individual MO columns rather than to exchange complete arrester banks once the spare columns are used. This matter was addressed in this contribution as well.
Awareness of the worldwide increasing use of line arresters was the reason to develop a dual logo IEC/IEEE standard on all types of line arresters, which is on a good way and may be published in a couple of years.
Summarized, MO surge arresters are mature devices today with an excellent service record. Major challenges have been solved during the recent years, and only a few items are open for future work. It must be a major concern now to maintain the very high technical and quality level of surge arresters. This is addressing manufacturers, standardization bodies, but also users who should not underestimate the expertise required for correct arrester application.
Acknowledgment
Prof. Hinrichsen expresses thanks to Max Reinhard, Maximilian Tuczek, Thomas Heinz, Moritz Gießel, Maike Bröker, Yvonne Späck-Leigsnering, and Peter Hock, who made it possible to learn the lessons, as reported here, by their Ph.D. projects, carried out at Technische Universität Darmstadt.
1 References
[1] CIGRE TB 696, MO surge arresters – Metal oxide resistors and surge arresters for emerging system conditions, CIGRE, 2017.
[2] IEEE C62.11-1987, IEEE Standard for Metal-Oxide Surge Arresters for AC Power Circuits, IEEE Standard, 1987.
[3] IEC 99-4, First Edition, 1991-11, Surge arresters – Part 4: Metal-oxide surge arresters without gaps for a.c. systems, IEC Standard, 1991.
[4] IEC 60099-4:2014, Surge arresters – Part 4: Metal-oxide surge arresters without gaps for a.c. systems, IEC standard, 2014.
[5] IEC 60099-9:2014, Surge arresters – Part 9: Metal-oxide surge arresters without gaps for HVDC converter stations, IEC Standard, 2014.
[6] IEC 60099-8:2017, Surge arresters – Part 8: Metal-oxide surge arresters with external series gap (EGLA) for overhead transmission and distribution lines of a.c. systems above 1 kV, IEC Standard, 2017.
[7] IEC 60099-5:2018, Surge arresters – Part 5: Selection and application recommendations, IEC Standard, 2018.
[8] IEC 60099-6:2019, Surge arresters – Part 6: Surge arresters containing both series and parallel gapped structures – System voltage of 52 kV and less, IEC Standard, 2019.
[9] IEEE C62.11-2012, IEEE Standard for Metal-Oxide Surge Arresters for AC Power Circuits (>1 kV), IEEE Standard, 2012.
[10] IEEE C62.22-2009, IEEE Guide for the Application of Metal-Oxide Surge Arresters for Alternating-Current Systems, IEEE Standard, 2009.
[11] IEC TC37, PT60099-11, “https://www.iec.ch/dyn/www/f?p=103:14:14791354044797::::FSP_ORG_ID:22209,” [Online]. [Accessed 2nd September 2019].
[12] CIGRE TB 544, MO Surge Arresters – Stresses and Test Procedures, CIGRE, 2013.
[13] K. G. Ringler, P. Kirkby, C. C. Erven, M. V. Lat and T. A. Malkiewitz, “The energy absorption capability and time-to-failure of varistors used in station-class metal-oxide surge arresters,” IEEE Transactions on Power Delivery, vol. 12, no. 1, 1997.
[14] M. N. Tuczek and V. Hinrichsen, “Recent Experimental Findings on the Single and Multi-Impulse Energy Handling Capability of Metal–Oxide Varistors for Use in High-Voltage Surge Arresters,” IEEE Transactions on Power Delivery, vol. 29, no. 5, 2014.
[15] M. Tuczek, Experimental Investigations of the Multiple Impulse Energy Handling Capability of Metal-Oxide Varistors for Applications in Electrical Power Engineering, Ph.D. Thesis, Technische Universität Darmstadt, https://tuprints.ulb.tu-darmstadt.de/8455/, 2015.
[16] C. M. Franck, “HVDC Circuit Breakers: A Review Identifying Future Research Needs,” IEEE Transactions on Power Delivery, vol. 26, no. 2, pp. 998 – 1007, 2011.
[17] T. Heinz, Gleichstromschalten in der Mittel- und Hochspannungstechnik unter Einsatz von Vakuumschaltröhren, Ph.D. Thesis, TU Darmstadt, https://tuprints.ulb.tu-darmstadt.de/6805/, 2017.
[18] P. Hock, N. Belda, V. Hinrichsen and R. Smeets, Investigations on Metal-Oxide Surge Arresters for HVDC Circuit Breaker Applications, INMR World Congress: Tucson, Arizona, USA, 2019.
[19] T. Jinzenji and al., “Development of Zinc Oxide Ceramic Energy Absorbers,” IEEE Transactions on Power Apparatus and Systems, vol. PAS 101, no. 5, pp. 1429-1436, 1983.
[20] M. Bröker and V. Hinrichsen, “Testing Metal-Oxide Varistors for HVDC Breaker Application,” IEEE Transactions on Power Delivery, vol. 34, no. 1, pp. 346 – 352, 2019.
[21] IEC 60143-2:2012, Series capacitors for power systems – Part 2: Protective equipment for series capacitor banks, IEC Standard, 2012.
[22] M. N. Tuczek, M. Bröker, V. Hinrichsen and R. Göhler, “Effects of Continuous Operating Voltage Stress and AC Energy Injection on Current Sharing Among Parallel-Connected Metal–Oxide Resistor Columns in Arrester Banks,” IEEE Transactions on Power Delivery, vol. 30, no. 3, pp. 1331-1337, 2015.
[23] R. Göhler and al., “Special Requirements on Surge Arrester Design for UHV A.C. Systems above 800 kV System Voltage,” in Cigre Session, Report A3-104-2010, Paris, 2010.
[24] V. Hinrichsen and M. N. Tuczek, “Surge arresters for insulation coordination in UHV power systems – related problems and solutions,” e&i Elektrotechnik & Informationstechnik, vol. 129, no. 5 (DOI: 10.1007/s00502-012-0032-1), pp. 326-331, 2012.
[25] V. Hinrichsen, M. Giessel and M. N. Tuczek, “Thermal Stability of HV and UHV Arresters with Reduced Grading Systems,” in INMR World Congress on Insulators, Arresters, Bushings & Cable Accessories, Munich, 2015.
[26] M. Giessel, Elektrothermisches Verhalten von Hochspannungs-Metalloxid-Ableitern mit reduzierten Steuersystemen in Wechselspannungsnetzen, Ph.D. Thesis, Technische Universität Darmstadt, https://tuprints.ulb.tu-darmstadt.de/8337/, 2019.
[27] Y. Späck-Leigsnering, Electrothermal Modeling, Simulation and Optimization of Surge Arresters, Ph.D. Thesis, Technische Universität Darmstadt, submitted 2019, to be published in 2019, https://tuprints.ulb.tu-darmstadt.de/cgi/search/advanced.
[28] Y. Späck-Leigsnering, E. Gjonaj and H. De Gersem, “Electrothermal Optimization of Field Grading Systems of Station Class Surge Arresters,” IEEE Journal on Multiscale and Multiphysics Computational Techniques, vol. 4, pp. 29-36, 2019, DOI: 10.1109/JMMCT.2019.2896630.